Question

найдите площадь квадрата диагональ которого равна 12√2
РЕБЯТА, СРОЧНО ПОМОГИТЕ!!!​

Answer 1

Ответ:

Пошаговое объяснение:

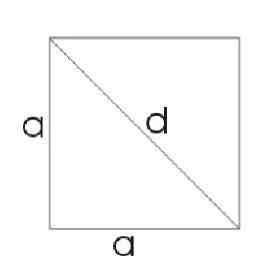
Диагональ квадрата d со стороной a будем считать гипотенузой прямоугольного треугольника с катетами a.

По теореме Пифагора:

d² = a² + a² = 2a²

Найдем сторону квадрата:

$[begin{gathered} 2{a^2}={left({12sqrt 2}right)^2}hfill \ 2{a^2}=288hfill\ {a^2}=288:2hfill \ {a^2}=144hfill \ a=sqrt {144}hfill \ a=pm 12hfill \ end{gathered} ]$

a = -12 - не подходит

a = 12 - сторона квадрата

S = a² - площадь квадрата

S = 12² = 144 ед²

Answer 2

Ответ: пусть сторона квадрата равна х, тогда диагональ равна √(х^2+x^2)=12*√2⇒√(2*x^2)=12*√2⇒x*√2=12*√2⇒x=12 единиц. Тогда площадь квадрата 12*12=144 квадратных единиц.

Пошаговое объяснение: