ПОМОГИТЕ, КАК ЭТО СДЕЛАЛИ? Ну ниже вы увидите условие помогите как это объяснить? Как они сделали так?
Условие
Известно, что биссектриса угла делит противолежащую сторону на отрезки, пропорциональные прилежащим к углу сторонам. Поэтому СЕ : ВЕ = АС : АВ = 1/2.
Тогда СЕ = 1/3 * ВС = 2√3 (см) и ВЕ = 2/3 *ВС = 4√3 (см)
Ответы
Задача:
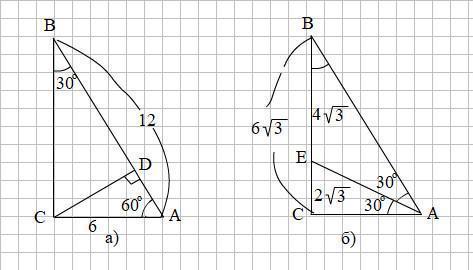
В прямоугольном треугольнике ABC угол C =90° угол B=30°, AB=12 см, CD- высота.
а)Докажите, что треугольник ACD подобен треугольнику ABC, найдите отношение их площадей б)отрезки, на которые биссектриса угла A делит катет BC
Объяснение:
а)Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны. Значит ΔАСД подобен ΔАВС:, т.к. ∠Д=∠С=90 , ∠А=∠общий. Найдем коэффициент подобия к=АС/АВ, к=6/12, к=1/2.
Отношение площадей подобных треугольников равно квадрату коэффициенту подобия: S(АСД):S(АВС)=к² , S(АСД):S(АВС)=1/4 .
б)
Найдем стороны в ΔАВС :
СА=1/2 АВ по св.угла 30, СА=6.
СВ²=АВ²-СА² по т. Пифагора, СВ²=144-36=108, СВ=√108=6√3.
Биссектриса внутреннего угла треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам:
СЕ:СА=ВЕ:ВА .
Пусть СЕ=х, ВЕ=6√3-х
х:6 =(6√3-х):12
6√3-х=2х
6√3=3х
х=2√3 т.е СЕ=2√3, ВЕ=6√3-2√3=4√3