Question

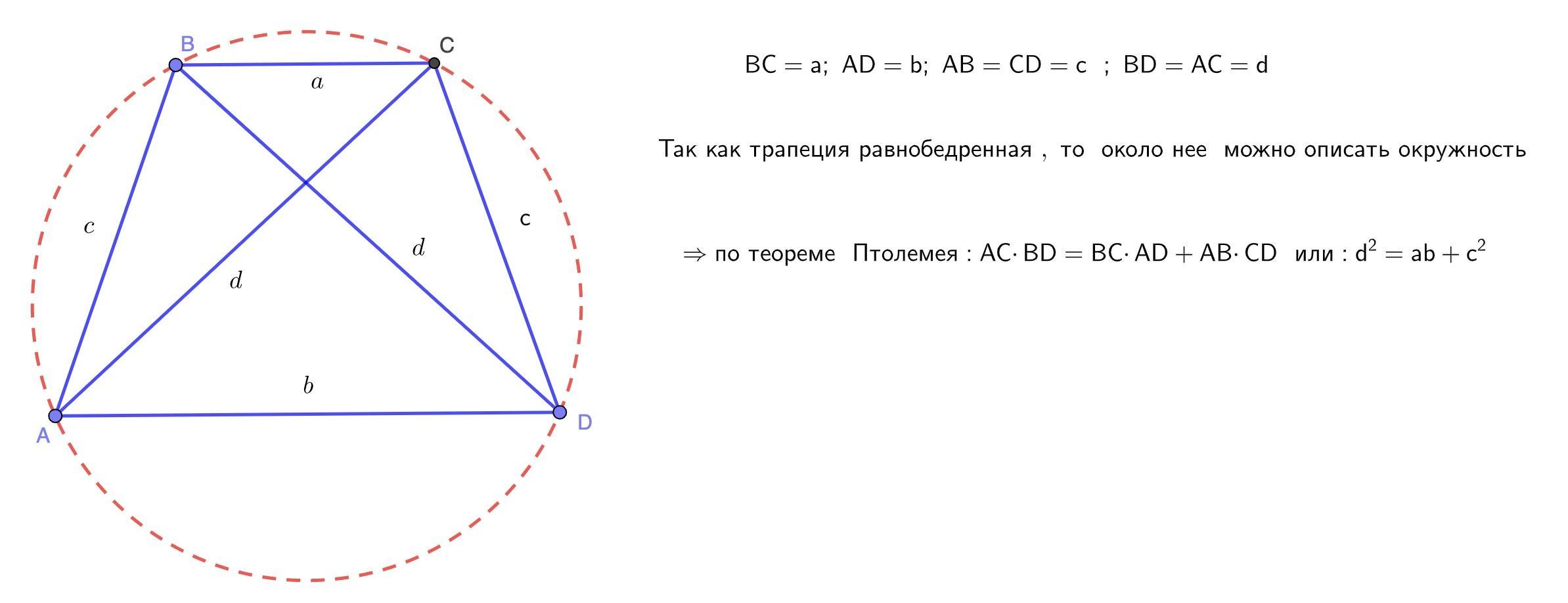
Основания равнобедренной трапеции равны а и b, боковая сторона равна с, а диагональ равна d. Доказать, что d² = ab + c²​

Answer 1

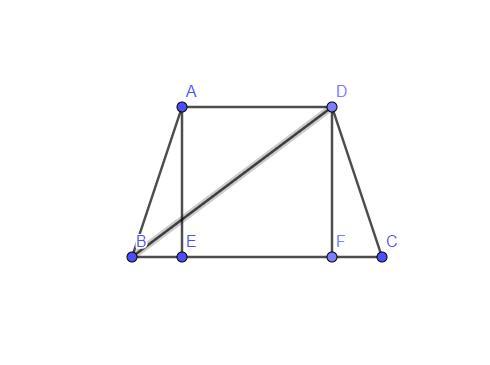
Итак. Давайте построим нашу трапецию с диагональю, при этом достроив высоты АЕ и DF.

FC = BC - BF

FC = (b - a)/2

Из треугольника FDC по т.Пифагора выразим DF:

DF² = DC² - FC²

DF² = c² - ((b - a)/2)²

$DF = sqrt{c^{2}-(frac{b-a}{2}) ^{2} }$

BF = b - (b - a)/2 = (2b - b +a)/2 = (b + a) /2

BD² = DF² + BF²

$BD^{2} = (sqrt{c^{2}-(frac{b-a}{2}) ^{2} })^{2} + (frac{b+a}{2}) ^{2}$

$BD^{2} = frac{b^{2} +2ab+a^{2} }{4}+c^{2} -frac{b^{2} -2ab+a^{2}}{4}$

$BD^{2} = frac{b^{2}+2ab+a^{2}+4c^{2} -b^{2} +2ab-a^{2} }{4}$

$BD^{2} = frac{4ab+4c^{2} }{4}$

BD² = ab + c²

А BD - и есть диагональ нашей трапеции. А значит:

d² = ab + c²

ЧТД

Answer 2

Решение : ///////////////////////////