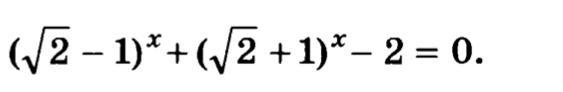Ответы
Ответ дал:
0
(√2-1)^x+(√2+1)^x -2=0
заменим √2-1=1/(√2+1)
t=(√2-1)^x >0
t+1/t-2=0
t²-2t+1=0
(t-1)²=0
t=1
(√2-1)^x=1
(√2-1)^x=(√2-1)^0
x=0
Ответ дал:
0
Замена происходит так :
Вас заинтересует
2 года назад
3 года назад
8 лет назад
8 лет назад