Ответы
Ответ дал:
0
Решение : //////////////////////////
Приложения:
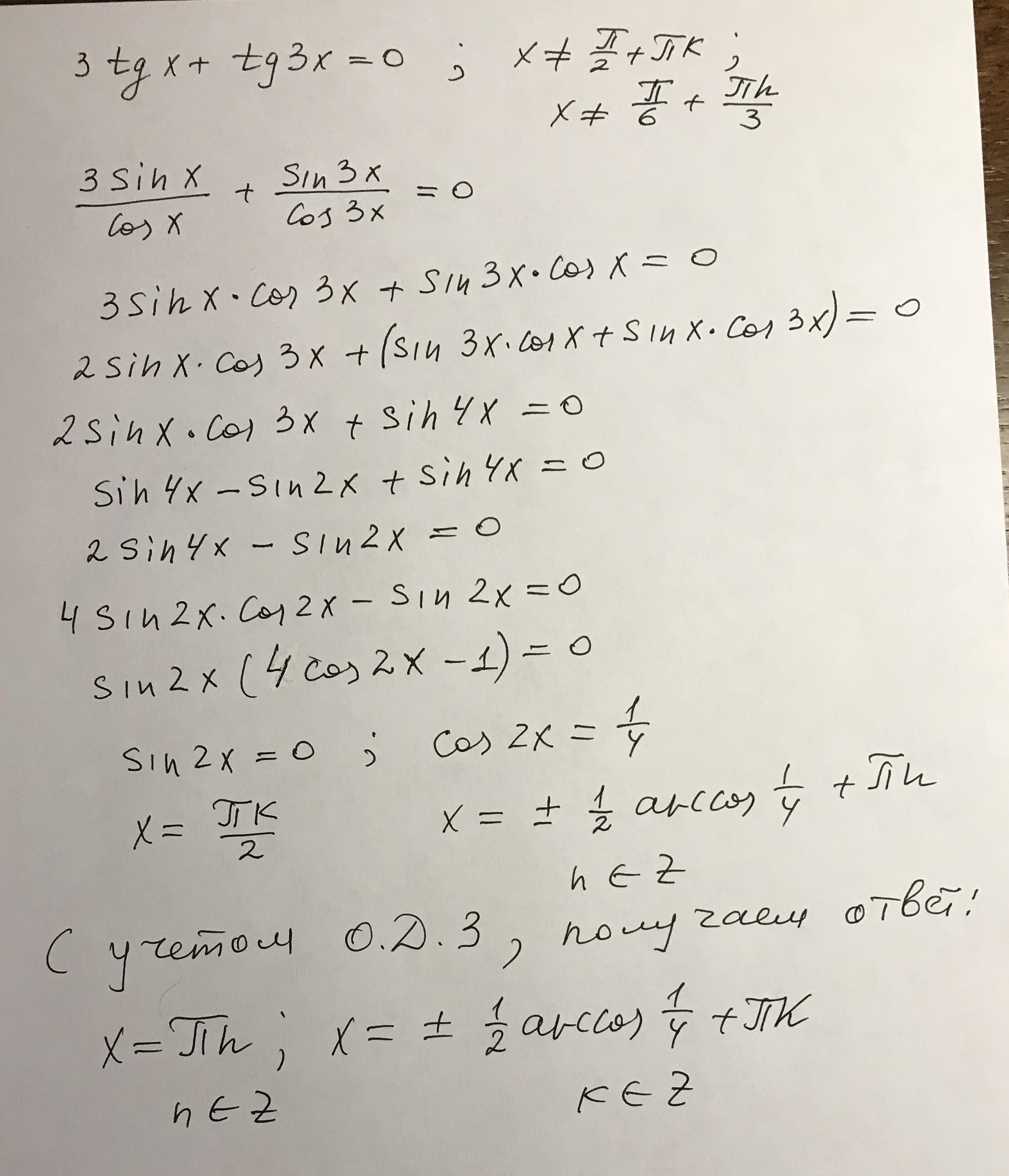
Ответ дал:
0
Сразу рассмотрим случай ;
Тогда видно, что является решением.
Теперь ;
Разделим обе части на :
; Воспользуемся формулой суммы тангенсов:
;
Но ; Подставляя это в уравнение, получаем:
;
Ну и заключительный этап:
, откуда получаем:
; Запишем ответ (переведя арккосинус в арктангенс):
Приложения:
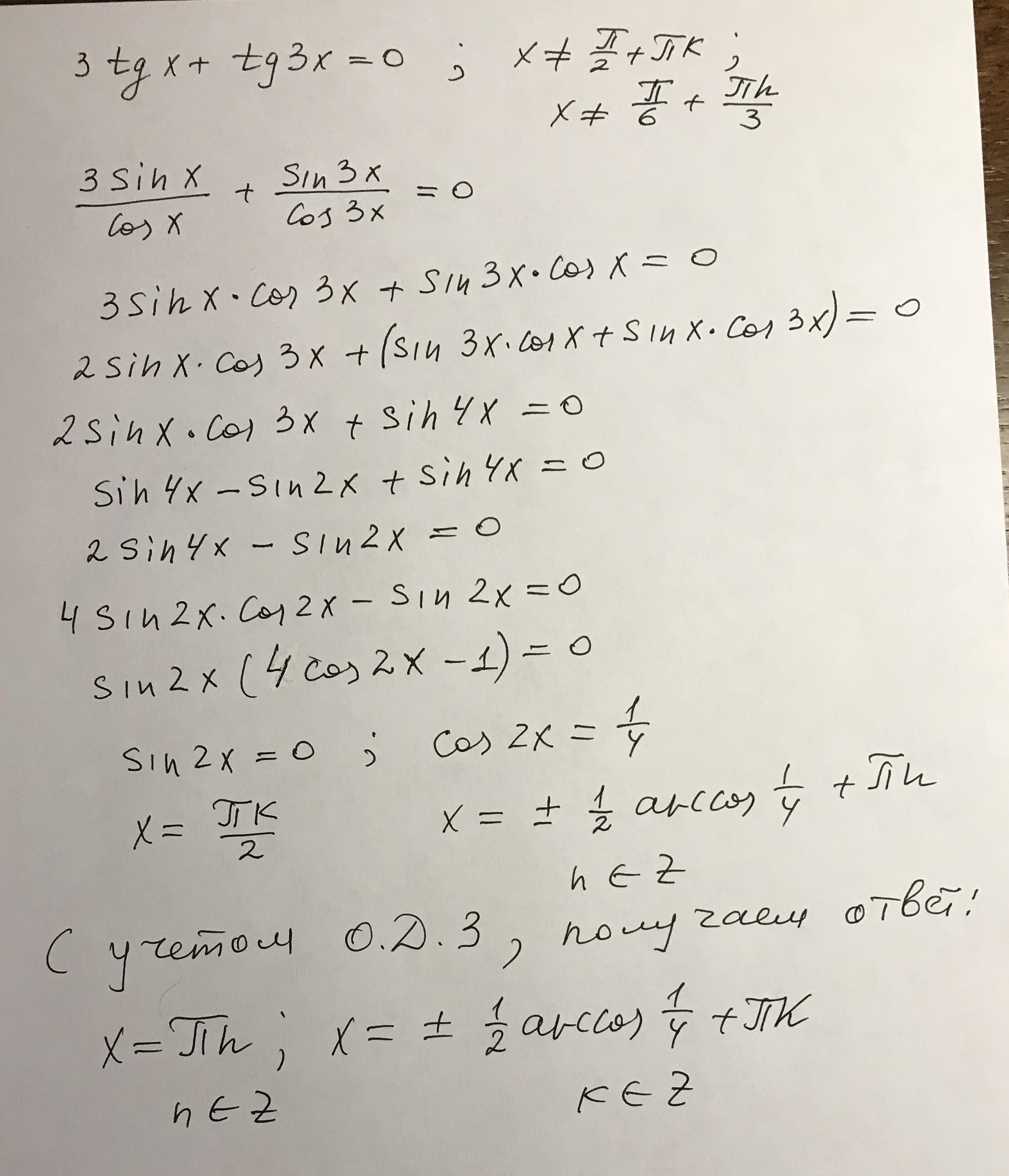
Ответ дал:
0
все верно , только pit/2 из ответа надо убрать ( pik уже есть , а pi/2 + pik не может быть по условию
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
9 лет назад