ВЫЗЫВАЮ ПОЯСНИТЕЛЬНУЮ БРИГАДУ!1!1!
ЕГЭ Проф. математика.
Есть собственно решение, но почему так, объясните пжлста
В правильной четырёхугольной пирамиде SABCD высота SH в два раза меньше диагонали основания. Точка К делит боковое ребро SA в отношении 1:2, считая от вершины А. Найдите угол наклона прямой КН к плоскости основания пирамиды.
Приложения:
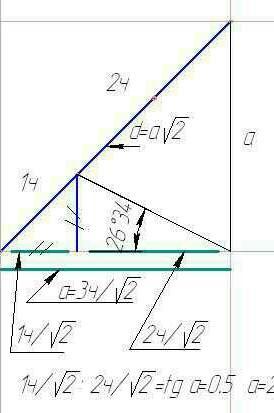
Ответы
Ответ дал:
0
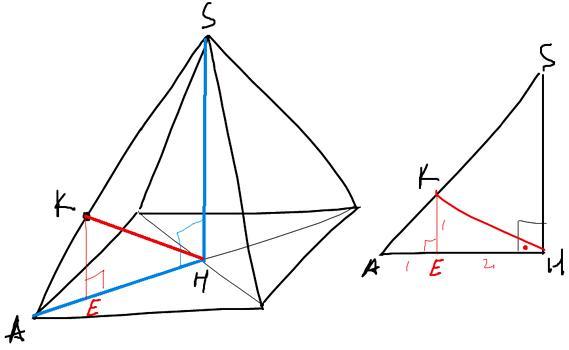
Правильная пирамида, вершина проецируется в центр описанной окружности основания. В основании квадрат, H - точка пересечения диагоналей. Диагонали квадрата равны и точкой пересечения делятcя пополам. SH=AH, AHS - равнобедренный.
Плоскость ASH перпендикулярна основанию (проходит через перпендикуляр SH), наклонная KH лежит в этой плоскости, дальнейшее решение в этой плоскости.
Опустим перпендикуляр KE на AH, KE||SH. По теореме Фалеса AE/EH=1/2, кроме того AE=KE (AEK~AHS).
tg(KHA) =KE/EH =1/2
Приложения:
Вас заинтересует
2 года назад
9 лет назад