Question

Биссектриса угла при основании равнобедренного треугольника делит боковую сторону на отрезки 10 см и 15 см, начиная от вершины. Найти периметр треугольника.

Answer 1

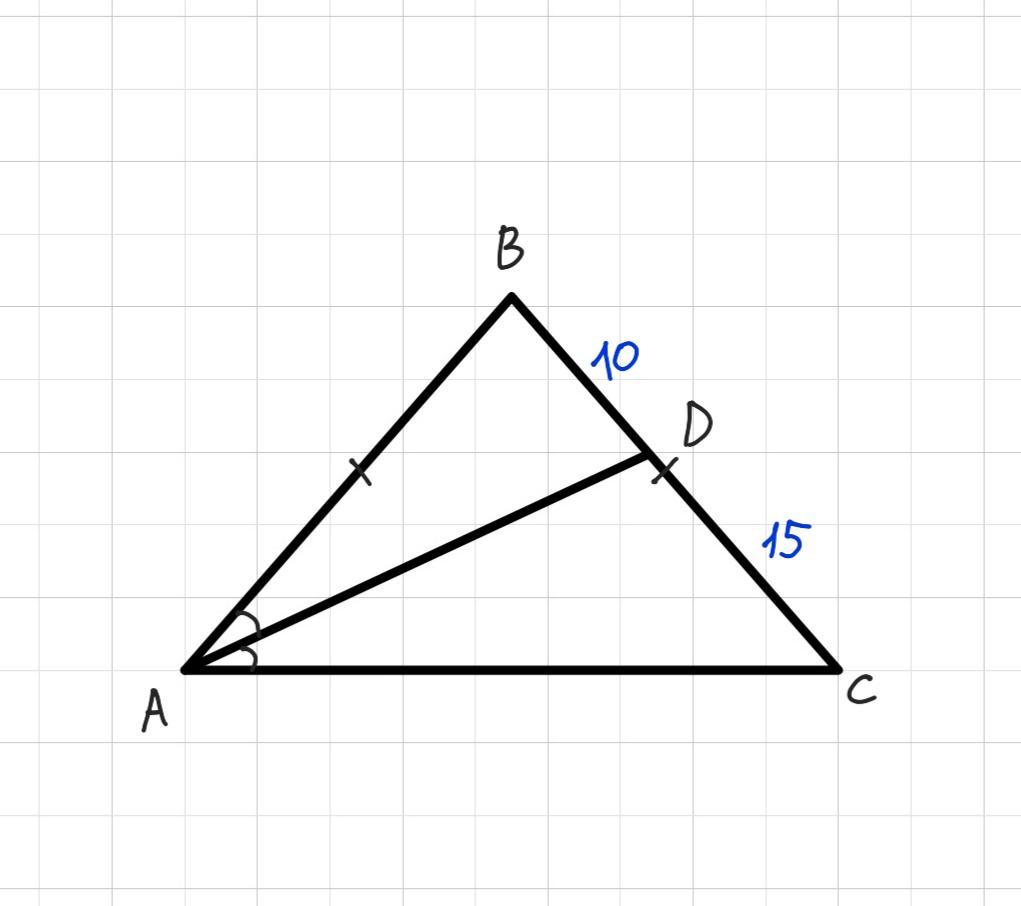
Дано: ΔABC - равнобедренный, АВ=ВС, AD - биссектриса, BD= 10 см, CD= 15 см.

Найти: Рabc.

Решение.

Так как по условию BD= 10 см, CD= 15 см, то ВС= BD+CD= 10+15= 25 (см).

Поскольку АВС - равнобедренный треугольник, то AB=BC= 25 см.

По свойству биссектрисы угла треуголька:

биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.

Т.е. AB : BD = AC : CD;

25:10= AC:15;

AC= 25•15 : 10;

AC= 37,5 (см).

Находим периметр треугольника АВС:

Рabc = AB+BC+AC= 25+25+37,5= 87,5 (см).

ОТВЕТ: 87,5 см.

Answer 2

Пожалуйста)