252. Найдите площадь равнобедренной трапеции, если: а) ее ос-
нования и боковая сторона соответственно равны 11 см, 17 см
и 5 см; б) известны ее основания 8 см, 2 см и угол 60°. С рисунком пожалуйста.
Ответы
Ответ дал:
0
Ответ:
а) 56 кв. см;
б) ... .
Объяснение:
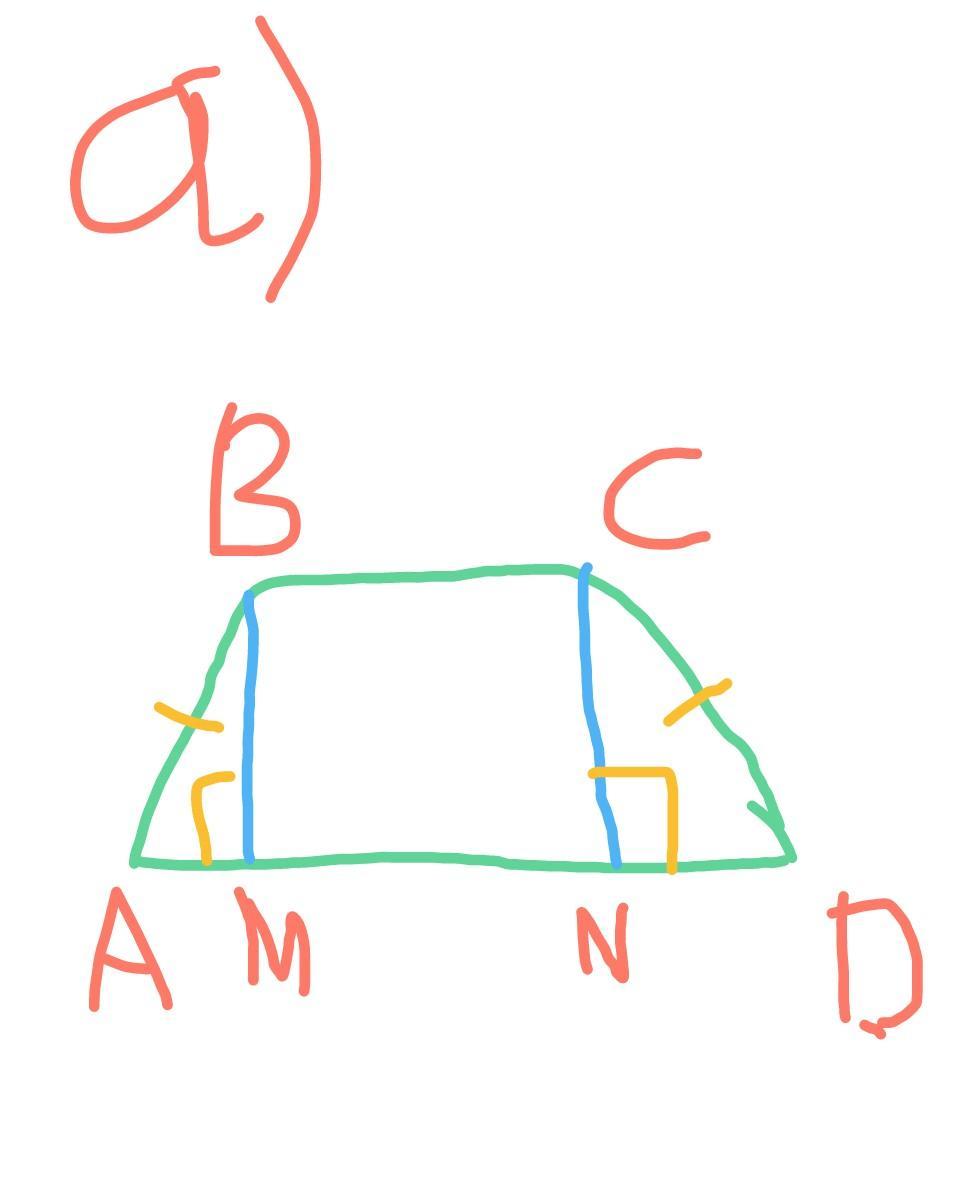
а) Дано:
АВСD - р/б трапеция;
АВ=CD=5 см (боковые стороны);
AD и BC - основания ABCD;
АВ=17 см;
ВС=11 см;
BM и CN - высоты АВСD.
Найти: S (ABCD).
Решение:
1) Рассмотрим прямоугольник (т. к. ВМ и CN - высоты АВСD) МВСN:
- ВC=MN=11 см (как противоположные стороны параллелограмма) => АМ=DN=(AD-MN):2= (17 см - 11 см) : 2 = 6 см : 2 = 3 см.
2) Рассмотрим прямоугольный треугольник (т. к. ВМ - высота) АВМ:
- По теореме Пифагора: высота ВМ^2=АВ^2-АМ^2=5^2-3^2=25-9=16 => ВМ = корень из 16 = 4 см.
3) Теперь можем найти площадь трапеции ABCD:
- S (ABCD)= 1/2•(AD+BC)•BM= 1/2 • (17 см + 11 см) • 4 см = 1/2 • 28 см • 4 см = 14 см • 4 см = 56 кв. см.
Ответ: 56 кв. см.
б) Дано:
АВСD - р/б трапеция;
АВ=CD (боковые стороны);
AD и BC - основания ABCD;
АВ=8 см;
ВС=2 см;
Угол АDC=60°;
BM и CN - высоты АВСD.
Найти: S (ABCD).
Решение:
1) ... .
Приложения:
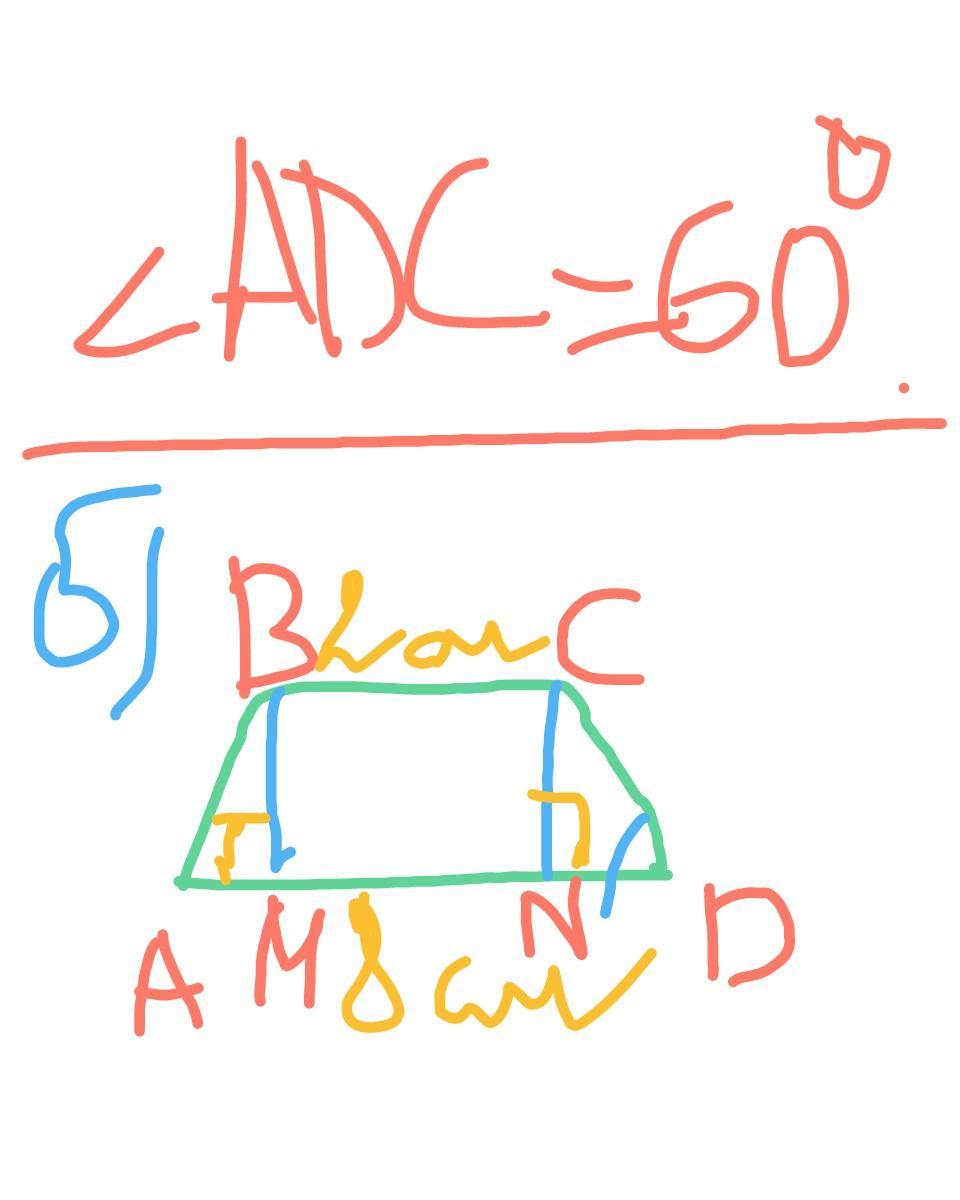
Ответ дал:
0
Вторую задачу думаю, но чёт как-то не могу решить.
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад