Question

ПОМОГИТЕ ПОЖАЛУЙСТА!! СРОЧНО НАДО
ДАЮ 100 БАЛЛОВ!!!​

Answer 1

Ответ:

Объяснение:

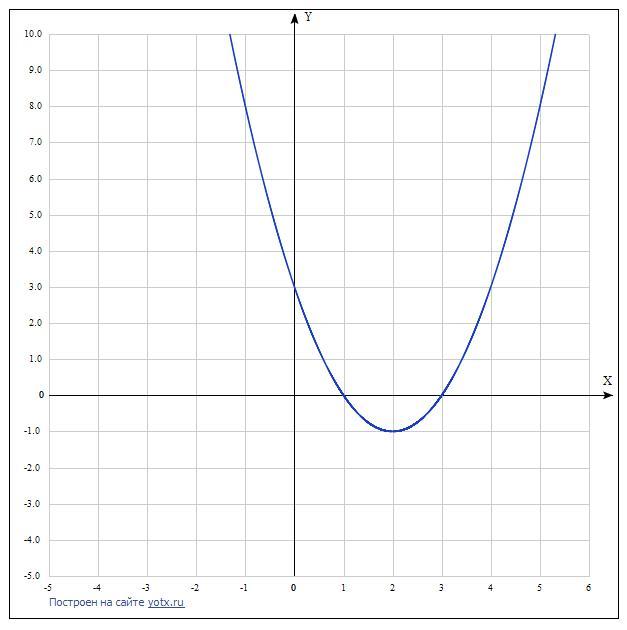
у=х²-4х+3

1)Это парабола ,ветви вверх. Координаты вершины

х₀=-b/2а,   х₀=-(-4)/2=2 , у₀=4-8+3= -1,    (2; -1).

2)Точки пересечения с осью ох , т.е. у=0

х²-4х+3=0  D=b²-4aс,   D=(-4)²-4*1*3=16-12=4   х=(-в±√D):2а , х=3 , х=1, значит (3;0)  (1;0)

3)Точки пересечения с осью оу , т.е. х=0

у(0)=0-0+3=3  (0;3)

4)Доп.точки у=х² - 4х+3 :  

х: -2  -1   3  4

у:  15  8  0  3

Answer 2

извини, но я не очень понял. Я сам алгебру не плохо знаю, просто эту функцию не понял и по алгоритму какомо-ту. Вот и хочу понять

Answer 3

Ответ:

Объяснение:

Исследуем функцию :

у=х²-4х+3 квадратичная функция,

график- парабола, ветви направлены вверх,т.к. а=1>0.

Найдём координатывершины параболы:

 m= -в/2а=4/2=2;   n=2²-4*2+3= -1;

 (2; -1) -координаты вершины параболы, х=2 - ось симметрии.

1) Область определения D(у): х∈(-∞ ;+∞ );

2) Область значений Е(у): у∈[-1;+∞);

2) Пересечение с осями координат.

  с ОХ:  х₁=1, х₂=3   ( х²-4х+3=0; по теореме Виета

                                  х₁х₂=3 и х₁+х₂=4 ⇒ х₁= -3, х₂=1 ),

  с ОУ:  у=3             (при х=0 у=0-0+3=3);

3) Чётность функции:

у(-х)= (-х)²-4(-х)+3=х²+4х+3,  у(-х)≠у(х) и у(-х)≠ -у(х) ⇒

функция не является ни чётной, ни  нечётной. (График функции не симметричен оси ОУ и не симметричен относительно начала координат)

4) Промежутки знакопостоянства функции:

  у>0 при х∈(-∞;1)∪(3:+∞),

  у<0 при х∈(1;3);

5) Промежутки монотонности функции:

  у возрастает при х∈[2;+∞),

  у убывает при х∈(-∞:2];

6) Функция не периодична.

7) Наименьшее значение функции у min= -1.