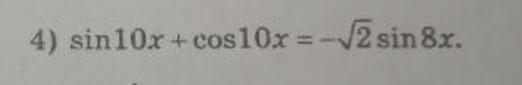Question

Помогите решить уравнение sin10x+cos10x=-√2sin8x

Answer 1

$4) sin(10x) + cos(10x) = - sqrt{2} sin(8x) \ sin {}^{2} (10x) + cos {}^{2} (10x) = 2 sin {}^{2} (8x) \ 2 sin{}^{2} (8x) = 1 \ sin {}^{2} (8x) = frac{1}{2} \ frac{1 - cos(16x) }{2} = frac{1}{2} \ 1 - cos(16x) = 1 \ cos(16x) = 0 \ 16x = frac{pi}{2} + 2pi n : : : : n in : z \ x = frac{pi}{32} + frac{1}{8} pi n : : : : n in : z$

Answer 2

левая часть должна же по формуле сокр.умножения раскрываться(а+b)^2. В общем потеряно удвоенное произведение; + 2sin(10x)cos(10x) (в левой части)