Question

Используя теорему Чевы, доказать, что в произвольном треугольнике прямые, проходящие через вершины и делящие периметр треугольника пополам, пересекаются в одной точке.

Answer 1

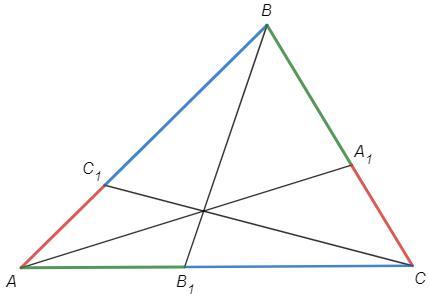
p - полупериметр

BA1 = p-AB = AB1

CB1 = p-BC = BC1

AC1 = p-AC = CA1

BA1 *CB1 *AC1 = AB1 *BC1 *CA1

следовательно чевианы AA1, BB1, CC1 проходят через одну точку.

Answer 2

A1, B1, C1 - точки касания вневписанных окружностей.

Answer 3

Точка Нагеля (N), точка пересечения медиан (M), центр вписанной окружности (I) лежат на прямой Нагеля.
NM : MI = 2:1