Question

|х+7| больше 8
ответьте пожалуйста
даю 10 баллов​

Answer 1

Решение и ответ на фото↓

Пользуйся на здоровье!)))

Answer 2

Вот полный ответ))

Answer 3

$|x + 7| > 8$

1 способ

Неравенства вида $|x| > a$ выполняются в таком случае:

$left[begin{array}{ccc}x > a, \x < -a\end{array}right$

Поэтому заданное неравенство равносильно совокупности:

$left[begin{array}{ccc}x + 7 > 8, \x + 7 < -8\end{array}right$

$left[begin{array}{ccc}x > 1, \x < -15\end{array}right$

Следовательно, решением данного неравенства будет $x in (-infty; -15) cup (1; +infty)$

2 способ

Возведем обе части неравенства в квадрат:

$|x + 7|^{2} > 8^{2}$

Так как $|x|^{2} = x^{2}$, то

$(x + 7)^{2} > 64$

$x^{2} + 14x + 49 - 64 > 0$

$x^{2} + 14x - 15 > 0$

Найдем нули данного выражения:

$x^{2} + 14x - 15 = 0$

$left{begin{array}{ccc}x_{1} + x_{2} = -14,\x_{1} cdot x_{2} = -15 \end{array}right$

$x_{1} =-15\x_{2} =1$

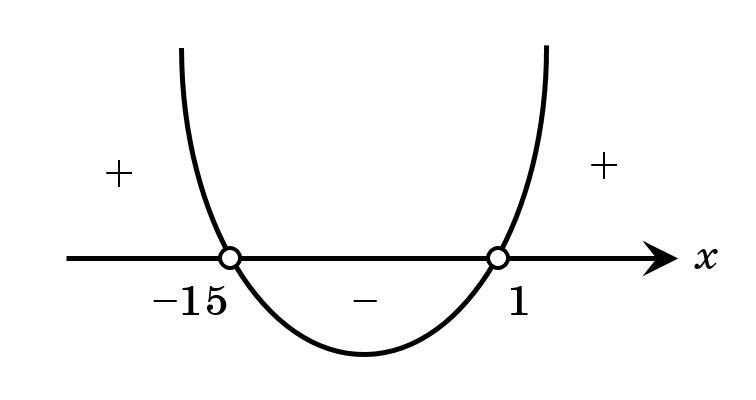
Имеем параболу с ветвями, направленными вверх и ее нулями в точках с абсциссами $x_{1} = -15$ и $x_{2} = 1$ (см. вложение). Квадратичная функция $y = x^{2} + 14x - 15$ находится выше оси абсцисс (то есть больше нуля) на промежутке $x in (-infty; -15) cup (1; +infty)$

Ответ: $x in (-infty; -15) cup (1; +infty)$