Question

Знайдіть синус гострого кута A, якщо cosA = 3/5

Answer 1

1 спосіб

Використовуючи основну тригонометричну тоточжність, маємо:

$sin^{2}alpha + cos^{2}alpha = 1$

$sin^{2}alpha = 1 - cos^{2}alpha$

$sin alpha = sqrt{1 - cos^{2}alpha }=sqrt{1 - left(dfrac{3}{5} right)^{2}} = sqrt{1 - dfrac{9}{25} } = sqrt{dfrac{16}{25} } = dfrac{4}{5}$

2 спосіб

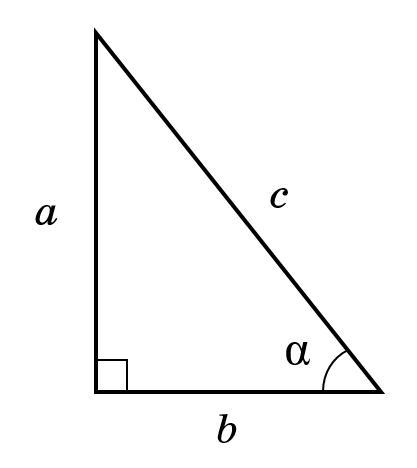
Нехай $a$ та $b$ — відповідно протилежний і прилеглий катети відносно кута $alpha$, а $c$ — гіпотенуза прямокутного трикутника (см. рисунок).

Косинусом госторого кута $alpha$ прямокутного трикутника називають відношення прилеглого катета $b$ до гіпотенузи $c$:

$cosalpha = dfrac{b}{c}$

Тобто $b = 3$, а $c = 5$ одиниць. Отже, за теоремою Піфагора $a = sqrt{c^{2} - b^{2}} = sqrt{5^{2} - 3^{2}} = sqrt{25 - 9} = sqrt{16} = 4$ одиниці.

Синусом госторого кута $alpha$ прямокутного трикутника називають відношення протилежного катета $a$ до гіпотенузи $c$:

$sin alpha = dfrac{a}{c} = dfrac{4}{5}$

Відповідь: $dfrac{4}{5}$