Question

Точки A и C расположены по одну сторону от прямой, к которой от обеих точек проведены перпендикуляры AB и CD равной длины. Определи величину угла∡ABC, если ∡ADB = 40°.

Answer 1

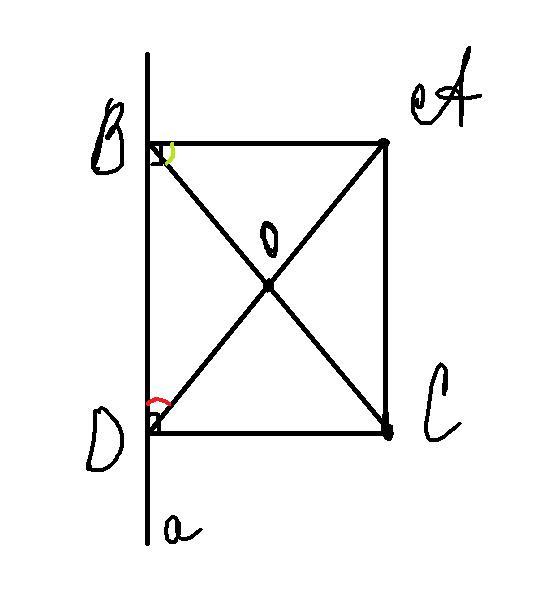
К решению прилагается рисунок

Дано:

a - прямая

AB,CD - перпендикуляры

∠ADB = 40°

Найти: ∠ABC

Решение: 1) Достроим ABCD до прямоугольника

Т.к. ABCD - прямоугольник ⇒ диагонали делятся пополам ⇒ AO = BO = OC = OD

2) Рассмотрим Δ BOD

Δ BOD - равнобедренный, т.к. BO = OD

У равнобедренного Δ углы при основании равны ⇒∠DBC =∠ADB = 40°

3) Рассмотрим Δ ABD

Т.к. AB - перпендикуляр ⇒ Δ ABD - прямоугольный

∠ABD = ∠DBC + ∠ABC ⇒ ∠ABC = ∠ABD - ∠DBC

∠ABC =  90° - 40° = 50°

Ответ: ∠ABC  = 50°