Question

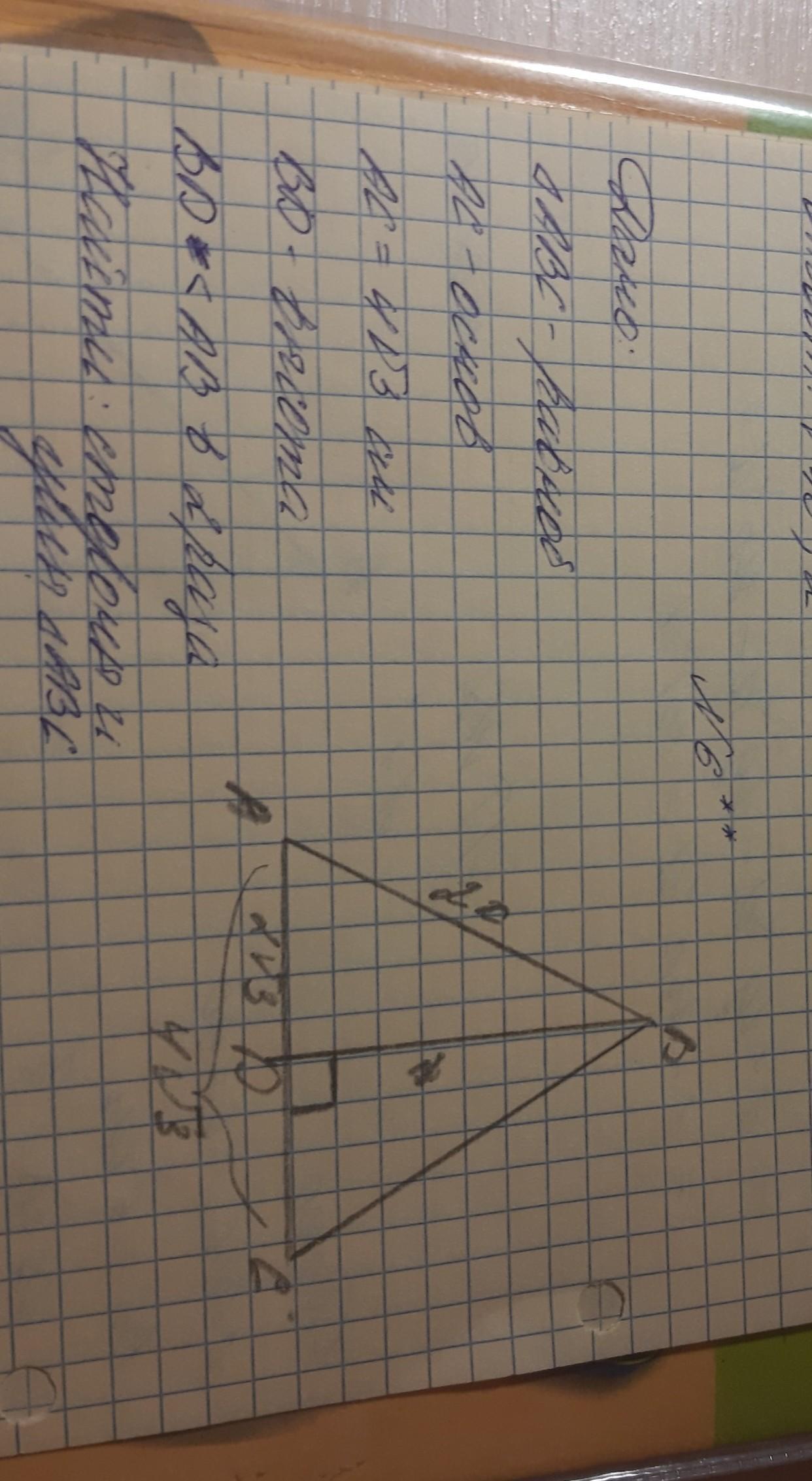
треугольник abc-равнобедренный ac-основание ac=4корень3 bd-высота bd больше ab в 2 раза найти стороны и углы треугольника​

Answer 1

Ответ:

Углы:

DAB=30°,DCB=30°,ABC=120°

Стороны:

AB=4 см,BC=4 см,AC=4 《3》 см

Объяснение:

1)Ищем углы в трехугольнике ABD.

• угол BDA =90° (ибо высота BD на стороне делает прямой угол)
• если катет BD меньше в два раз чем гипотенуза,то что мы знаем про угол DAB?Что он равен 30° ибо правило про катет гласит:катет,который лежит напротив 30° равняеться половине гипотенузы.С этого следует,что BD=2AB.В результате угол DAB=углу DCB= 30° (ибо трехугольник равнобедренный
• Тогда угол ABD 60° (180°-30°-90°=60°)
• Ищем высоту BD и сторону AB=BC (равнобедренный трехугольник) за теоремой Пифагора:

2x²=x²+2《3》² (《》-это корень)

4x²=x²+12

3x²=12

x²=4

x=2 высота BD

Тогда сторона AB=BC=2×2=4 (См)

• Ищем угол ABC

Углы DAB и DCB по 30°,тогда угол ABC=180-(30°+30°)=120°