Question

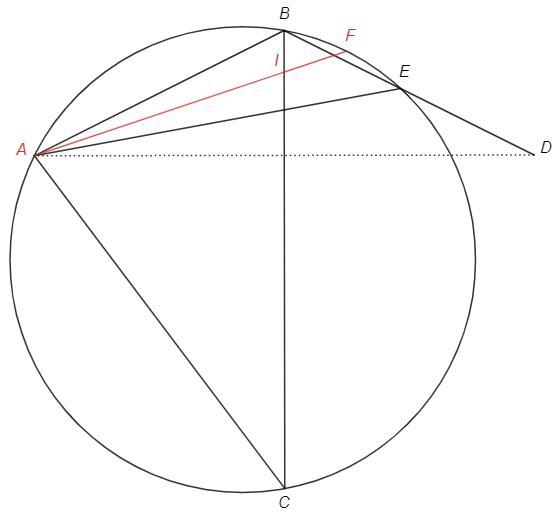
Про треугольник ABC известно, что AC=20, BC=22, а его площадь равна 132. Точка D симметрична A относительно BC, E — пересечение прямой BD и дуги BC описанной окружности треугольника ABC, не содержащей точку A. Пусть I — центр вписанной окружности треугольника ABE. Найдите квадрат длины отрезка AI.

Answer 1

ABC=DBC (симметрия) => ∪AC=∪EC

∪BF=∪FE (AI - биссектриса)

AIC =(∪BF+∪AC)/2 =(∪FE+∪EC)/2 =FAC

△ACI - равнобедренный

AI^2 =2AC^2(1-cosC)

132 =1/2 *20*22 *sinC => sinC =3/5

1) cosC = 4/5

AI^2 =800*1/5 =160

2) cosC = -4/5

AI^2 =800*9/5 =1440