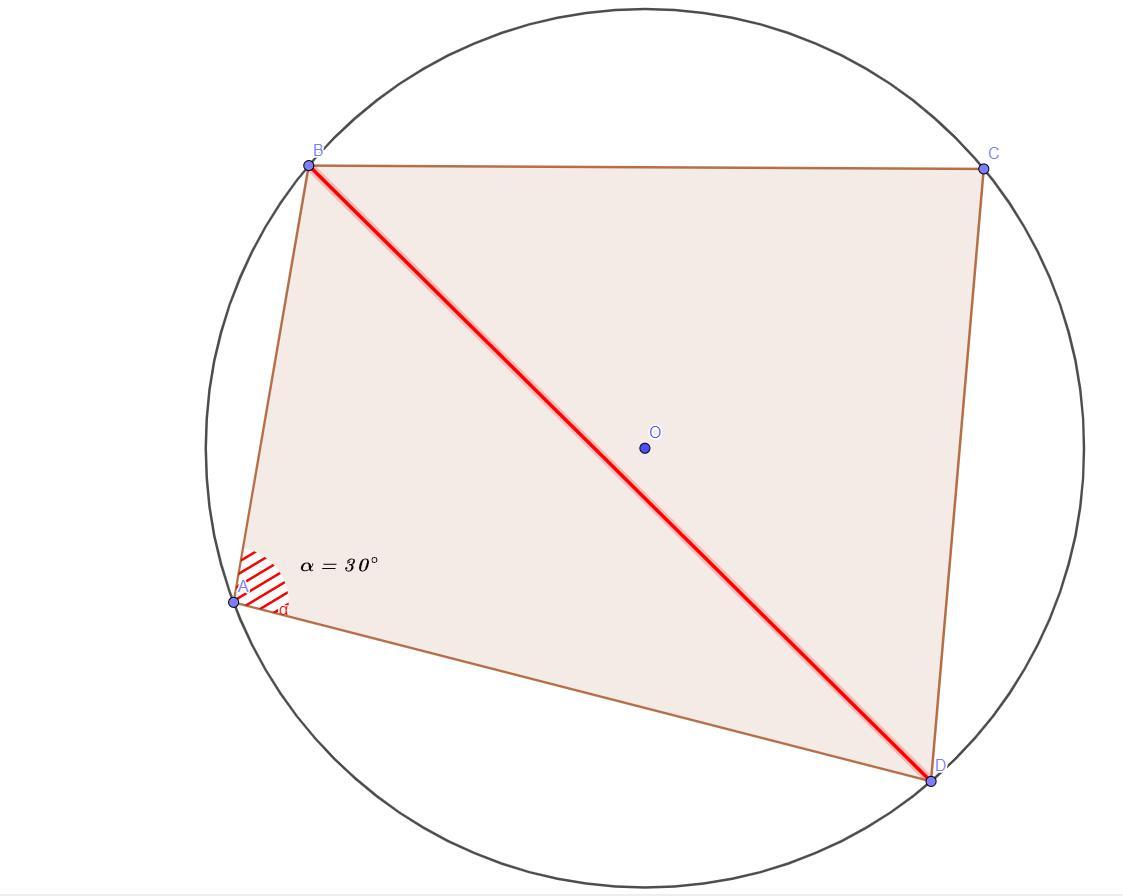
У коло, діаметр якого дорівнює корінь 12, вписано чотирикутник АВСD. Знайдіть діагональ BD, якщо кут BDA = 30 градусів.
Ответы
Ответ дал:
0
Відповідь:
BD = √3
Пояснення:
(див. малюнок до задачі)
1) Отож, маємо справу з вписаним чотирикутником. Для початку, давай я просто наведу одну єдину формулу чи то відношення, якою (яким) ми будемо користуватися:
1) a/sinα=b/sinβ=c/sinγ=2R - розширена теорема синусів (див. мал.). Цю Теорему будемо застосовувати до трикутника ABD, де <BAD = 30°.
2) Оскільки діаметр дорівнює подвоєному радіусу, то радіус дорівнює:
;
3) З трикутника ABD за пропорційністю сторони і протилежних кутів до цієї сторони (тобто за формулою!), маємо, що:
.
Приложения:
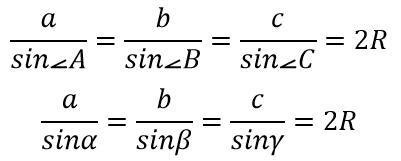
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад