Ответы
Ответ дал:
0
Ответ:
Объяснение:
чтобы найти точки минимума и максимума нужно сначала производную, потом приравнять к нулю
переведем выражение в натуральный логарифм будет F(x)=ln(x^2+16x+100)/ln7
найдем производную
F'(x)=1/ln7* (2x+16)/(x^2+16x+100)
приравняем к нулю
можно уже убрать постоянный множитель, потому что справа 0
2x+16/x^2+16x+100 =0
так как на ноль делить нельзя:
x^2+16x+100=/0
там дискриминант отрицательный
значит при любом x положительный ответ
2x+16=0
x=-8
чертим прямую, отмечаем закрашенную точку -8
проверяем, с крайне правого будет +, потом -
значит минимум- это точка -8
Ответ дал:
0
Ответ:
Объяснение:
Решаем через замену переменных.
Приложения:
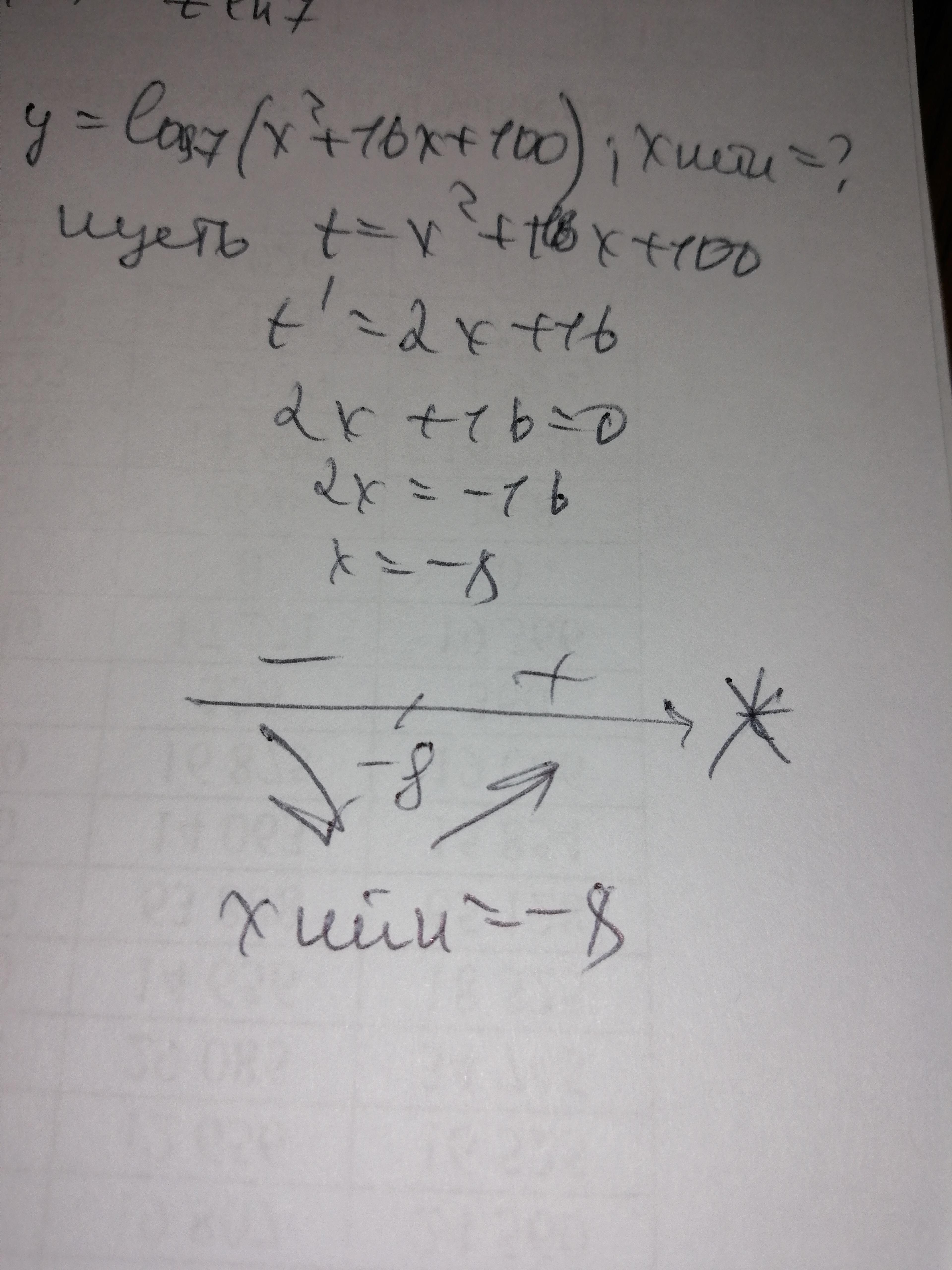
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад