Question

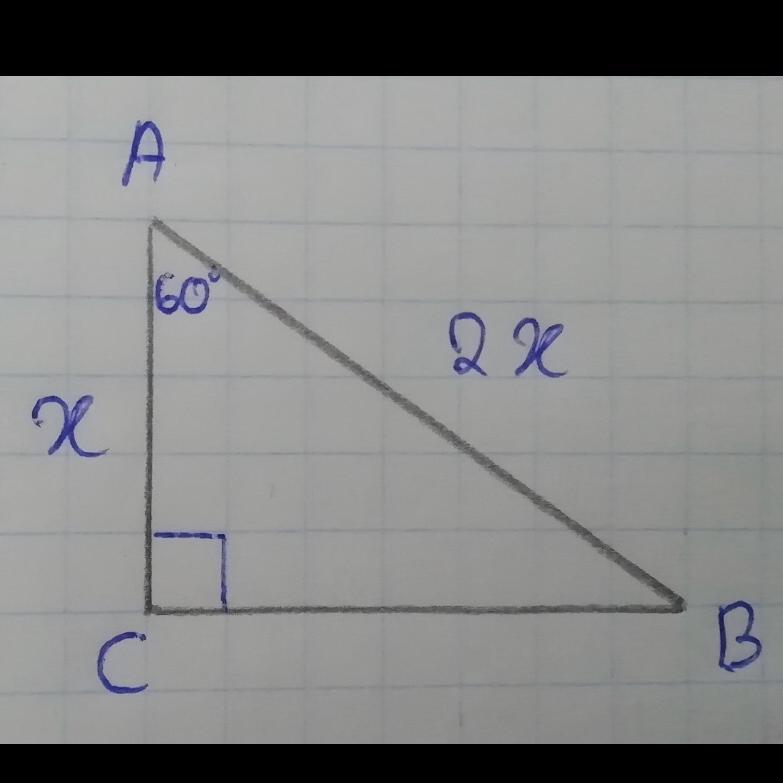
В прямоугольном треугольнике АВС ∠С = 90° , ∠А = 60° . Найдите
гипотенузу и меньший катет этого треугольника, если известно, что их сумма равна 27,9 см

Answer 1

Ответ:

1)∠В = 180°-(90°+60°)=30°

2) АС=1/2*АВ (т к находится напротив угла в 30°)

3) Обозначим за х- меньший катет, тогда 2х- то гипотенуза, зная что их сумма равна 27,9 , Составим и решим уравнение

х+2х=27,9;

3х=27,9;

х= 9,3, значит меньший катет равен 9,3 см(АС)

4) АВ=9,3*2=18,6(см)

Ответ: 9,3 см и 18,6 см.

Объяснение:

Answer 2

∠B = 90 - 60 = 30°  (сумма острых углов прямоугольного треугольника равна 90°)

Пусть x - меньший катет, тогда гипотенуза равна 2x, ведь катет лежит напротив угла в 30°, значит, равен половине гипотенузы. Получим уравнение

x + 2x = 27,9

3x = 27,9

x = 27,9/3 = 9,3 см - меньший катет

Гипотенуза равна 2x = 2 * 9,3 = 18,6 см

Ответ: 18,6 см, 9,3