Question

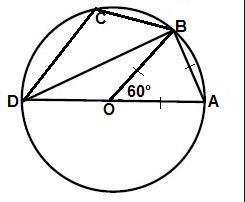
На окружности с центром O выбраны точки A, B, C и D так, что сторона АD четырехугольника АВСD является диаметром, а угол АОВ = 60°. Найдите угол ВСD. Ответ дайте в градусах.

Answer 1

Ответ:

120°.

Пошаговое объяснение:

1) ∆ BOA равнобедренный (ОB = ОА как радиусы одной окружности), тогда

∠ ОBА = ∠ ОАB (углы при основании равнобедренного треугольника).

Так как  ∠ АОB = 60°, то  ∠ ОBА + ∠ ОАB = 180° - 60° = 120°, каждый из них по 120°: 2 = 60°, ∆BOA равносторонний.

2) Четырёхугольник АВСD вписанный по условию, тогда сумма его противолежащих углов равна 180°:

∠ ОАB + ∠ ВСD = 180°

∠ ВСD = 180° - ∠ ОАB = 180°  -  60° = 120°.