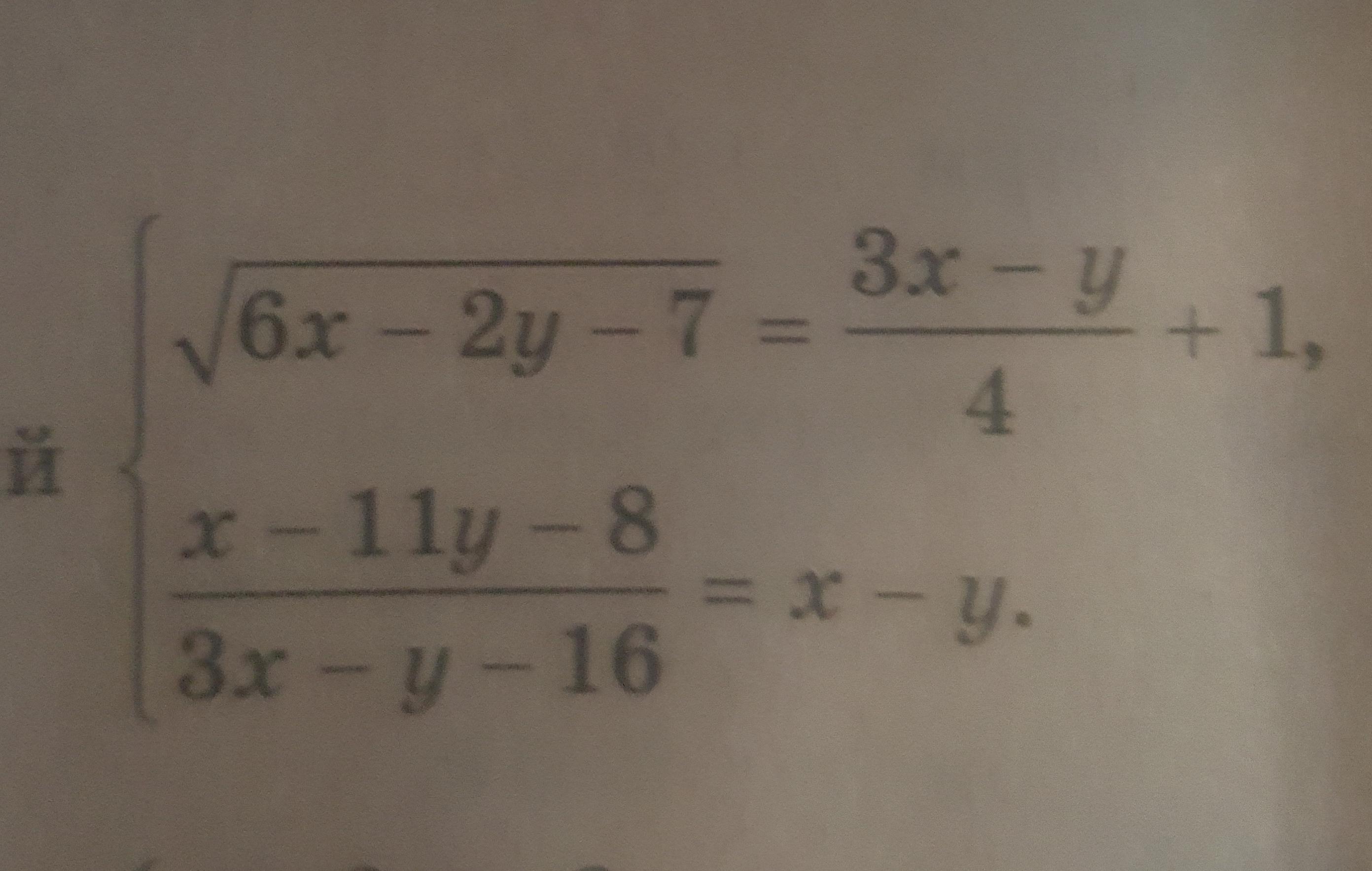Question

Решите систему уравнений

Answer 1

√(6x - 2y - 7) = (3x - y)/4 + 1

3x - y = t

√(2t - 7) = t/4 + 1

одз 2t - 7 ≥ 0 t ≥ 3.5

t/4 + 1 ≥ 0  t ≥ - 4

t ≥ 3.5

возводим в квадрат

2t - 7 = t²/16 + t/2 + 1

32t - 112 = t² + 8t + 16

t² - 24y + 128 = 0

D = 24² - 4*128 = 576 - 512 = 64

t12 = (24 +- 8)/2 = 16  8  оба корня проходят

подставляем во 2 уравнение

(x - 11y - 8)/(3x - y - 16) = x - y

1. t = 3x - y = 16

знаменатель получается 0

нет решений

2. t = 3x - y = 8

y = 3x - 8

( x - 33x + 88 - 8)/(3x - 3x + 8 - 16) = x - 3x + 8

-32x + 80 = 16x - 64

48x = 144

x = 3

y = 9 - 8 = 1

ответ (3, 1)

Answer 2

"t12 = (24 +- 8)/2 = 16 8 оба корня проходят"-прежде чем указывать на чужые ошибки........