Ответы
Примем систему координат в точке А, АВ по оси Оу, АД - по Ох.
Уравнение окружности примет вид (х - 6)² + (у - 6)² = 36.
Для уравнения прямой МВ найдём угловой коэффициент, равный тангенсу угла наклона этой прямой к оси Ох.
tg(-15°) = -tg(15°) = -(sin30°/(1 + cos30°)) = (-1/2)/(1+(√3/2)) = (-1/(2 + √3)) ≈ -0,267949.
Уравнение МВ: у = (-1/(2 + √3))*х + 12.
Для нахождения координат точки М решаем систему из двух уравнений - окружности и прямой МВ.
{(х - 6)² + (у - 6)² = 36,
{у = (-1/(2 + √3))*х + 12.
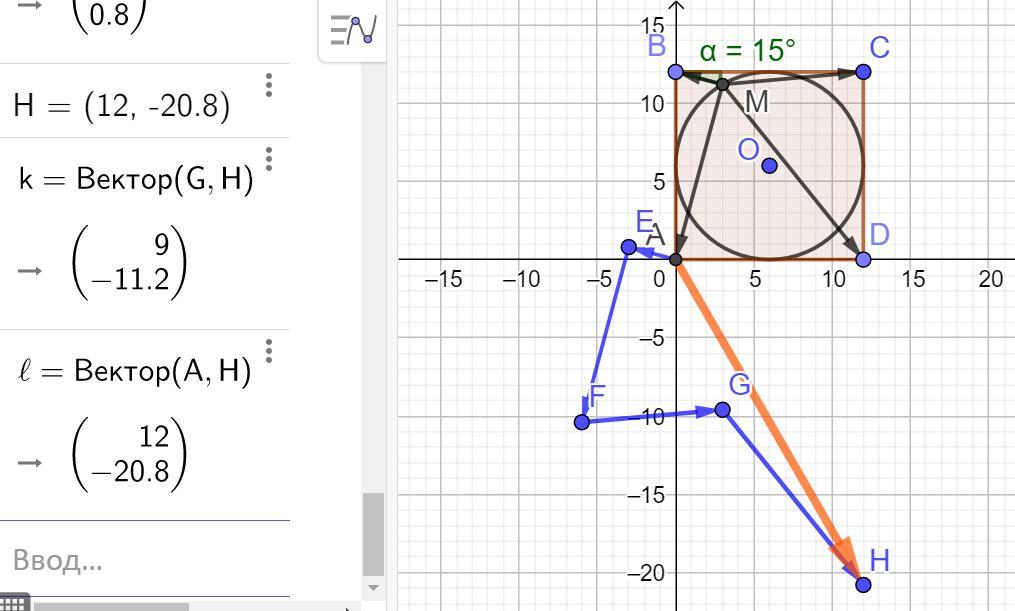
Получаем М(3; 11,2).
Находим координаты векторов:
МА = (-3; -11,2), МВ = (3; 0,8), МС = (9; 0,8) и МД = (9; -11,2).
Их сумма равна m = (12; -20,8).
Модуль (длина) суммы векторов - это длина вектора АН.
АН = √(12² + (-20,8)²) = 24,01333.
Ответ: длина суммы векторов равна 24,01333.