Question

Помогите!!! Решите неравенство sin x < cos x .
правильный ответ:
2πl + 5π/4 < x < 9π/4 + 2πl , l ∈ Z
как его получили объясните пожалуйста понятно

Answer 1

$sinx-cosx < 0$

$cosx=sin(frac{pi }{2} -x)$

$sinx- sin(frac{pi}{2} -x)<0$

$2sinfrac{x-(frac{pi }{2}- x) }{2} cdot cos frac{x+(frac{pi }{2}- x) }{2}<0\ \ 2sin(x-frac{pi }{4} )cdot cosfrac{pi }{4}<0\ \ sin(x-frac{pi }{4} ) <0\\-pi+2pi k <x-frac{pi }{4}<2pi k, k in Z\\-pi+frac{pi }{4}+2pi k <x< frac{pi }{4}+2pi k, k in Z\\-frac{3pi }{4}+2pi k <x< frac{pi }{4}+2pi k, k in Z$

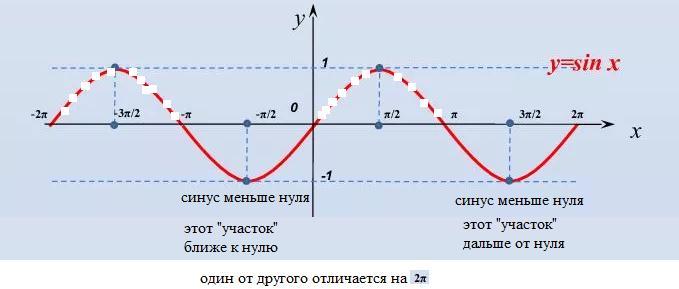
Этот промежуток ближе к нулю, чем тот, который в ответе.

Чтобы получить тот, который в ответе, надо прибавить 2π

$-frac{3pi }{4}+2pi+2pi k <x< frac{pi }{4}+2pi+2pi k, k in Z\ \ frac{5pi }{4}+2pi k <x< frac{9pi }{4}+2pi k, k in Z$

Или в процессе решения неравенства брать промежуток, который дальше от нуля справа ( см. рис):

$sin(x-frac{pi }{4} ) <0\\pi+2pi k <x-frac{pi }{4}<2pi+2pi k, k in Z\\pi+frac{pi }{4}+2pi k <x<2pi+ frac{pi }{4}+2pi k, k in Z\\frac{5pi }{4}+2pi k <x< frac{9pi }{4}+2pi k, k in Z$