Ответы
Ответ дал:
0
1.
Возводим в квадрат:
2.
не имеет корней, 2-√5 < 0
3.
Делим на 2
2|x+2|<x+5
2|x+5|≥0, поэтому при x+5 < 0 уравнение не имеет корней
При x+5 ≥0 возводим в квадрат:
4·(x+2)²<(x+5)²
4·(x²+4x+4) < x²+10x+25
3x²+6x-9<0
x^2+2x-3<0
D=4+12=16
x₁=-3; x₂=1
-3 < x < 1
С учетом х+5≥0
о т в е т. (-3;1)
4.
2сos²x=2·(1-sin²x)
Уравнение:
2·(1-sin²x)=|sinx|
2sin²x+|sinx|-2=0
D=1+16=17
|sinx|=(-1±√17)/4
|sinx|=(-1-√17)/4 не имеет корней (-1-√17)/4 < 0
|sinx|=(-1+√17)/4 ⇒
sinx=±(-1+sqrt(17))/4
sinx=(-1+sqrt(17))/4⇒ x=(-1)^(k) arcsin((-1+sqrt(17))/4)+πk, k∈Z - о т в е т.
sinx=-(-1+sqrt(17))/4⇒ x=(-1)^(m+1) arcsin((-1+sqrt(17))/4)+πm, m∈Z - о т в е т.
Объединяем оба ответа.
Ответ дал:
0
Ответ:
Объяснение:
!!!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:
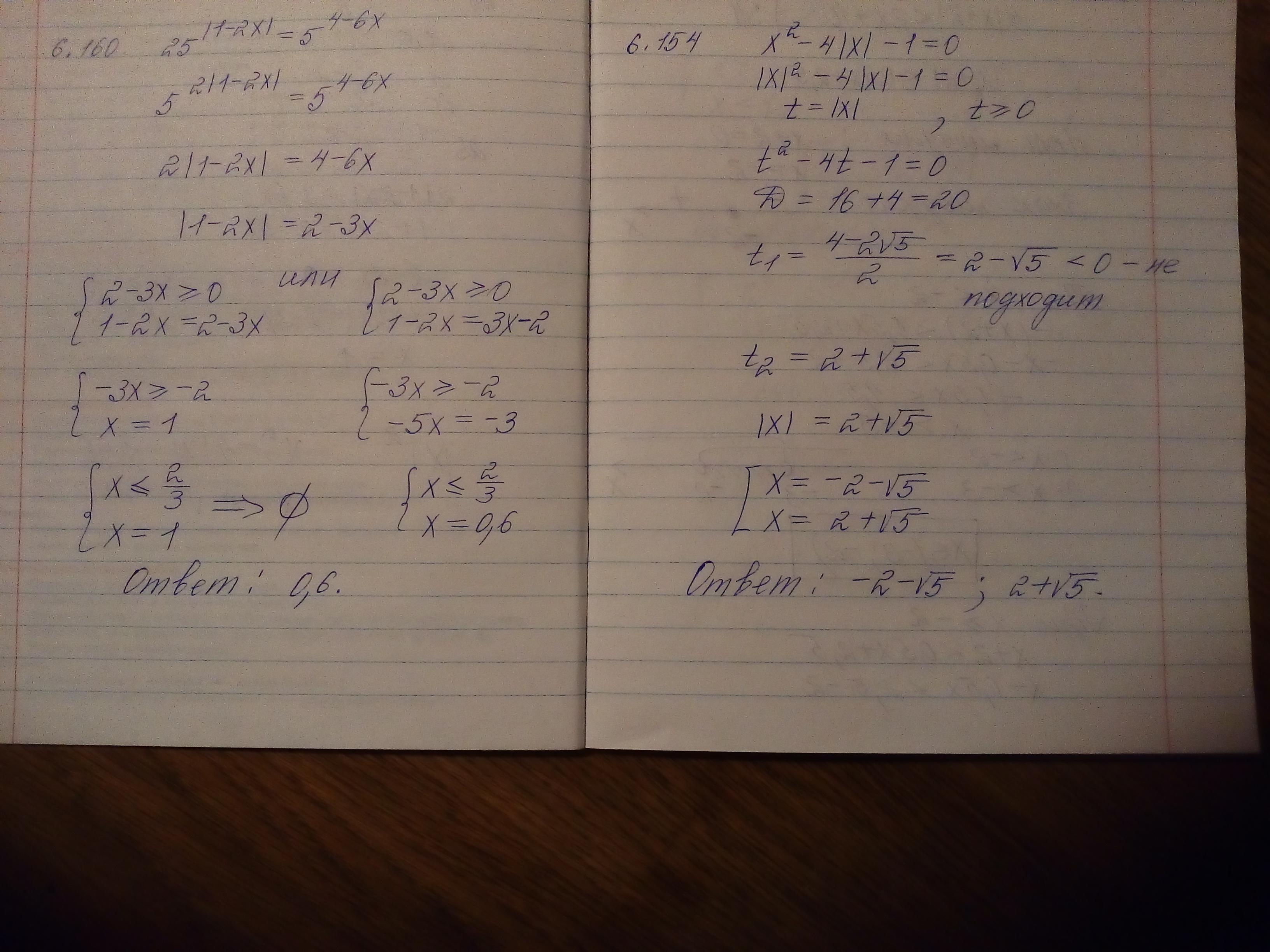


Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад