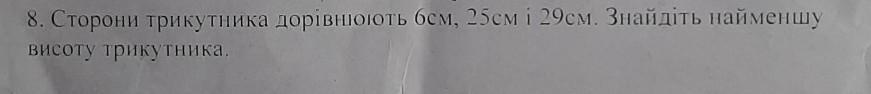Question

Допоможіть будь ласка. Ставлю 50 балів.​

Answer 1

Если даны три стороны, то можно найти углы треугольника по теореме косинусов.

Пусть a=6; b=25; c=29

b²=a²+c²-2·a·c·cos∠B

25²=6²+29²-2·6·29·cos∠B

cos∠B=(36+841-625)/(12·29)=21/29

BD=BC·cos∠B=6*(21/29)=126/29

По теореме Пифагора  из Δ BCD высота СD

CD²=BC²-BD²=6²-(126/29)²=36-(15876/841)=14400/841

CD=120/29

( можно найти sin∠B) и

тогда

CD=BC·sin∠B

Второй способ.

Найти площадь по формуле Герона:

$S=sqrt{p(p-a)(p-b)(p-c)}$

p=(a+b+c)/2 - полупериметр треугольника.

p=(6+25+29)/2=30

p-a=30-6=24

p-b=30-25=5

p-c=30-29=1

$S=sqrt{30cdot 24cdot 5cdot 1}=60$

Наименьшая высота проведена к наибольшей стороне.

$S=frac{ccdot h}{2} \ \ h=frac{2S}{c}=frac{120}{29}$