Question

Найти объем тела, полученного вращением вокруг оси ОХ фигуры, ограниченной астроидой


$left { {{x=a*cos^3(t)} atop {y=a*sin^3(t)}} right.$

Answer 1

$V=pi intlimits^a_b {f^2(x)} , dx$

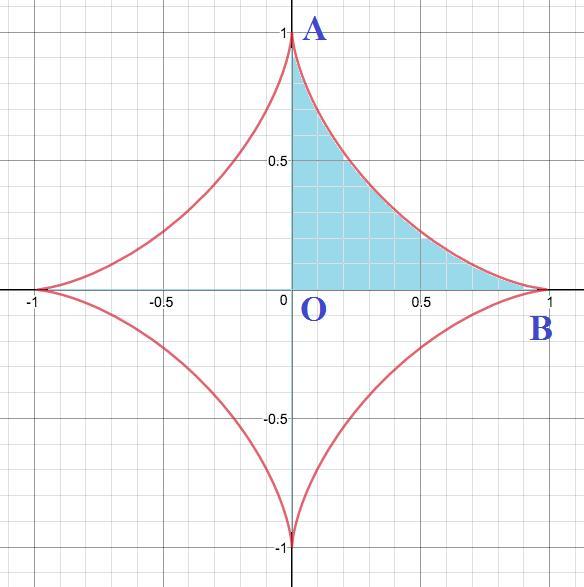
Так как астроида симметрична относительно оси Ох и Оу, то

вычислим половину объема, полученного вращением треугольника АОВ вокруг оси Ох  ( точке B соответствует значение параметра t=0; точке А  -  t=π/2)

$frac{1}{2} V=pi intlimits^0_{frac{pi }{2} } {(asin^3t)^2} , d(acos^3t)= pi a^3intlimits^0_{frac{pi }{2} } {(sin^6t}cdot 3cos^2tcdot(-sint) , dt= \ \ =-3pi a^3intlimits^{frac{pi }{2} }_0 {(1-cos^2t)^3 cdot cos^2td(cost)} , dt=frac{16 pi a^3 }{105}$

$V=frac{32pi a^3 }{105}$