Question

В треугольнике ABC уголA=45°, а высота BН делит сторону на отрезки АН и
НС соответственные равные 6 см и 10 см. Найдите площадь треугольника ABН.
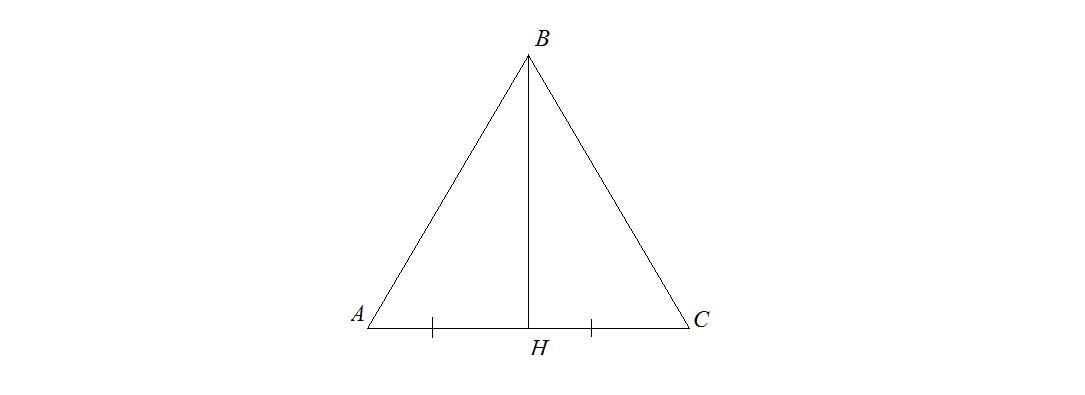
Выполнить рисунок.
Определить вид треугольника АВН.
Найти сторогу АС треугольника АВС.
Найти высоту треугольника АВС.
Найти искому площадь.​

Answer 1

Ответ:

Объяснение:

Пусть дан треугольник ABC,где угол А = 45 °. ВН-высота  ;

АН = 6 (см) , НС = 10 (см). Найдём  S треугольника.

Рассмотрим треугольник АВН : угол А = 45  ° (по условию), значит угол АВН = 45 °. Следовательно треугольник равнобедренный и АН = НС = 6 (см) ,найдём АС.

АС = АН + НС = 6 + 10 = 16 (см)

Рассмотрим ВН: в равнобедренному треугольнике высота, проведенная к основанию, является медианой и биссектрисой.

Найдём высоту по формуле ВН=1/2*АС.

ВН = 1/2 * 16 = 8 (см)

S тр. = S= 1/2 АС * ВН

S тр. = 1/2 *  16 * 8 = 64 (см)

Answer 2

Находим высоту через тангенс, а площадь через высоту и сторону