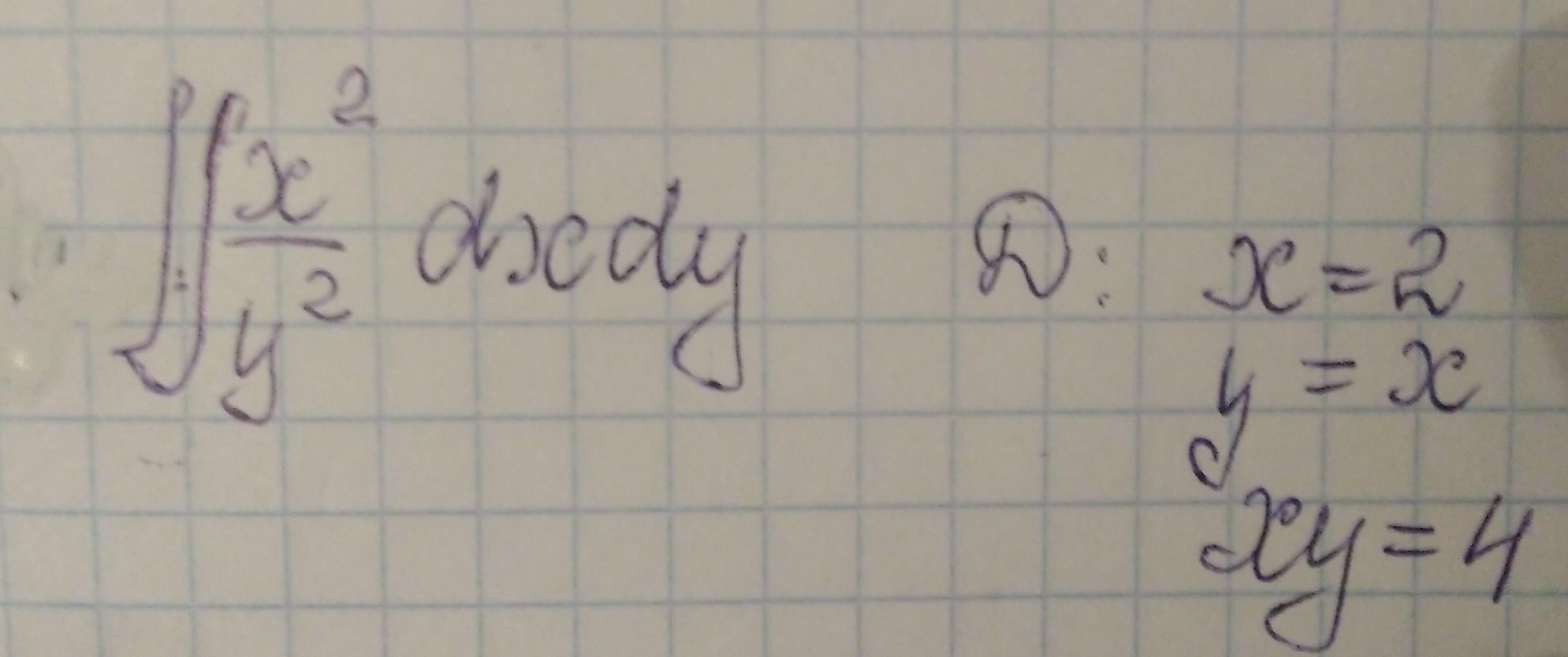Question

Задание на фотографии

Answer 1

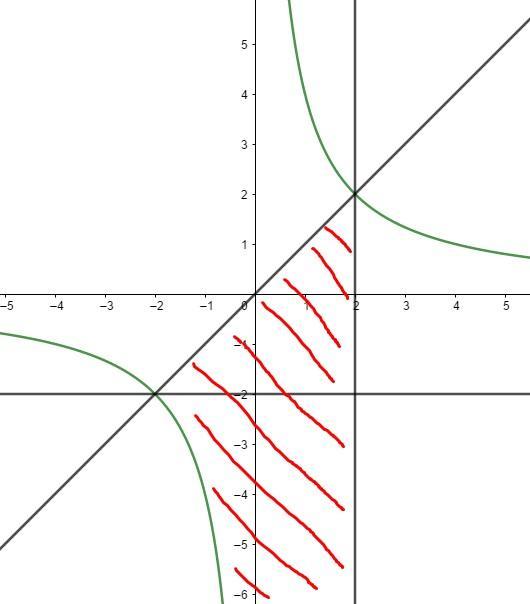
Наша область является неограниченной снизу и разобъем данную область прямой y = -2. Будем рассматривать как сумму двух интегралов

$displaystyle iintlimits_Ddfrac{x^2}{y^2}dxdy=intlimits^2_{-2}dyintlimits^{2}_ydfrac{x^2}{y^2}dx+intlimits^{-2}_{-infty}dyintlimits^2_{4/y}dfrac{x^2}{y^2}dx=intlimits^2_{-2}dfrac{x^3}{3y^2}bigg|^2_{y}dy+\ \ \ +intlimits^{-2}_{-infty}dfrac{x^3}{3y^2}bigg|^2_{frac{4}{y}}dy=intlimits^2_{-2}left(dfrac{8}{3y^2}-dfrac{y}{3}right)dy+intlimits^{-2}_{-infty}left(dfrac{8}{3y^2}-dfrac{64}{3y^5}right)dy=$

$displaystyle =left(-dfrac{8}{3y}-dfrac{y^2}{6}right)bigg|^2_{-2}+left(-dfrac{8}{3y}+dfrac{16}{3y^4}right)bigg|^{-2}_{-infty}=-dfrac{4}{3}-dfrac{2}{3}-dfrac{4}{3}+dfrac{2}{3}+dfrac{4}{3}+dfrac{1}{3}=\ \ \ =-dfrac{8}{3}+dfrac{5}{3}=-1$

Answer 2

$xy=4; x=dfrac 4y; lim_{y to -infty} dfrac 4y= -0$

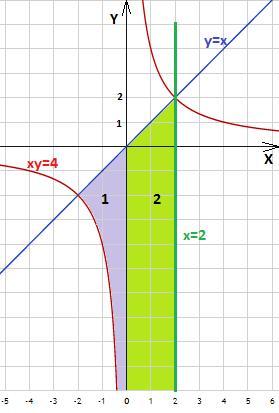
Область интегрирования можно разбить на две части :

1) x∈[-2;0) , снизу область ограничена гиперболой  y = 4/x, сверху прямой y=x   (на рисунке залита фиолетовым цветом )

2) x∈[0;2] , снизу область не ограничена, сверху ограничена прямой y=x   (на рисунке залита зелёным цветом )

$displaystyle1)~iintlimits_{D_1} {dfrac{x^2}{y^2}} , dx =intlimits^0_{-2} dx intlimits^x_{4/x} dfrac{x^2}{y^2} dy =intlimits^0_{-2} bigg(-dfrac{x^2}ybigg) bigg|^x_{frac 4x} dx =\\=-intlimits^0_{-2} bigg(dfrac{x^2}x-x^2:dfrac 4xbigg) dx =-intlimits^0_{-2} bigg(x-dfrac {x^3}4bigg) dx = \\=-bigg(dfrac {x^2}2-dfrac{x^4}{16}bigg)bigg|^0_{-2}=0+dfrac42-dfrac {16}{16}=1$

$displaystyle2)~iintlimits_{D_2} {dfrac{x^2}{y^2}} , dx =intlimits^2_0 dx intlimits^x_{-infty} dfrac{x^2}{y^2} dy =intlimits^2_0 bigg(-dfrac{x^2}ybigg) bigg|^x_{-infty} dx =\\=-intlimits^2_0 bigg(dfrac{x^2}x-(-0)bigg) dx =-intlimits^2_0 x dx = \\=-dfrac {x^2}2 bigg|^2_0=-dfrac42+0=-2$

$displaystyle~iintlimits_D {dfrac{x^2}{y^2}} , dx =iintlimits_{D_1} {dfrac{x^2}{y^2}} , dx+iintlimits_{D_2} {dfrac{x^2}{y^2}} , dx=1-2=-1$