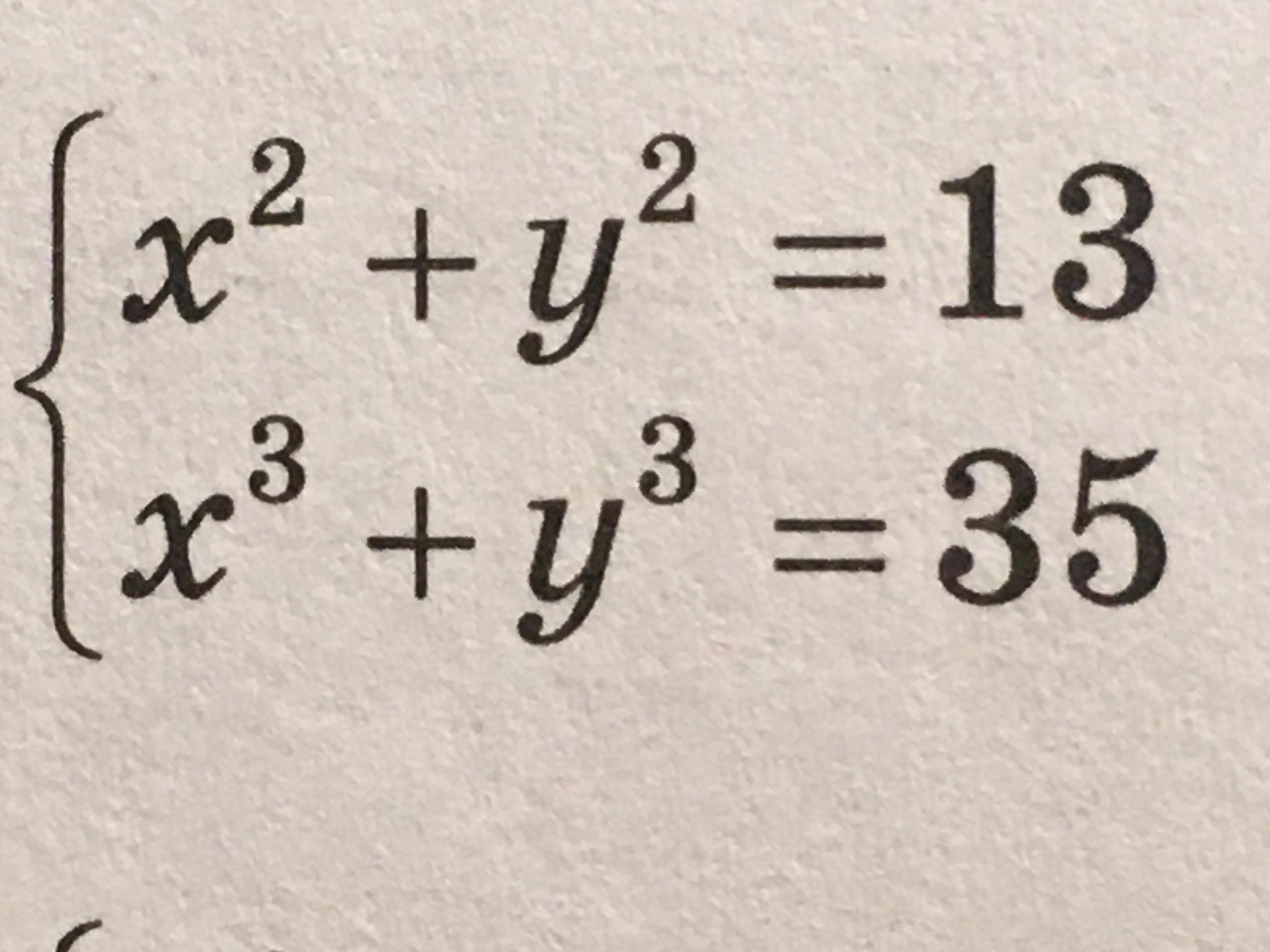Ответы
Ответ:
Четыре решения :
x=3 y=2
или
x=2 y=3
Другие два решения :
x=1+0,5*sqrt(22)
y=1-0,5*sqrt(22)
или
х=1-0,5*sqrt(22)
у=1+0,5*sqrt(22)
Пошаговое объяснение:
Сразу видим х=3 у=2, но надо помотреть какие еще корни :
Втрое уравнение : (x+y)(x^2+y^2-xy)=35
С учетом первого : (x+y)(13-xy)=13*(x+y)-xy*(x+y)=35
xy*(x+y)=13(x+y)-35
(x+y)^3-39(x+y)+105-35=0
Обозначив (х+у) за t
t^3-39t+70=0
t=5
(t-5)*(t^2+5t-14)=0 дискриминант квадратного трехчлена D=25+56=81
t^2+5t-14=(t+7)*(t-2)
(x+y)=5 (x+y)=-7 (x+y)=2
Для каждого (х+у)
x^2+y^2=13
x^2+y^2+2xy=25
2xy=12 (x-y)^2=1
Две системы :
x+y=5
x-y=1
x=3 y=2
Или
x+y=5
x-y=-1
x=2 y=3
(х+y)^2=49
2xy=36, что невозможно (квадрат разности будет меньше 0)
х+у=2
(х+y)^2=4
2ху=-9
(х-y)^2=22
x-y=sqrt(22)
x+y=2
x=1+0,5*sqrt(22)
y=1-0,5*sqrt(22)
Другая пара решений
х=1-0,5*sqrt(22)
у=1+0,5*sqrt(22)
Ответ:
Пошаговое объяснение: