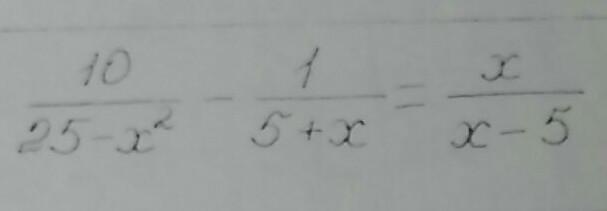Question

Помогите решить пожалуйста ​

Answer 1

Ответ:

-1

Объяснение:

Область допустимых значений:

x≠5, x≠-5

$frac{10}{25-x^{2} } -frac{1}{5+x} =frac{x}{x-5} \frac{10}{(5+x)*(5-x) } -frac{5-x}{(5+x)*(5-x)} =frac{x}{x-5} \\frac{1}{5-x } =frac{x}{x-5} \x(5-x)=x-5\x^{2} -5x+x-5=0$

$x^{2} -4x-5=0\x1=5, x2=-1$

Так как первый корень не входит в область допустимых значений, то остается только

x2=-1

Answer 2

Ответ:

х=-1

Объяснение:

х≠5 , -5

дробь $frac{10}{25-x^{2} }$ = $frac{10}{(5-x)5+x)}$

$frac{10-5+x+5x+x^{2} }{(5-x)(5+x)} =0$ (знак  дроби после знака равно поменяли и в знаменателе поменяли местами)

Опускаем знаменатель и решаем:

$x^{2}$+6x+5=0

По коэффициентам находим X:

1) x=-1 , 2) x=-5-не удовл. ОДЗ.

Ответ: х=-1