Question

ВЫЗЫВАЮ ПОЯСНИТЕЛЬНУЮ БРИГАДУ!1!1
ЕГЭ проф математика
1402 Заранее спасибо ​

Answer 1

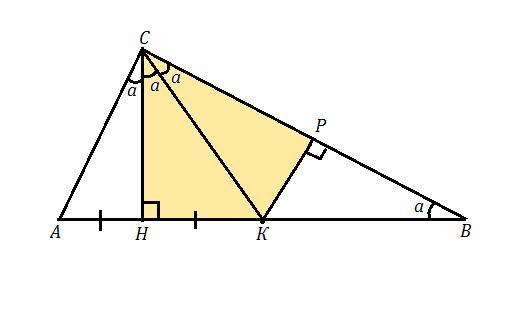
ΔАВС , СН⊥АВ , СК - медиана  ⇒  АК=ВК=1/2*АВ , ∠АСН=∠КСН=∠ВСК

S(ΔАВС)=1,5+√3 .  Найти радиус вписан. окружности r .

 Так как СН - высота и ∠АСН=∠КСН, то СН - биссектриса. А если в треугольнике биссектриса является ещё и высотой, то это возможно  только в равнобедренном треугольнике. Но по свойству равноб. треуг. СН ещё и медиана равнобедренного ΔАСК . Значит, АН=НК.

НК=АН=1/2*АК=1/2*ВК=1/2*(с/2)=с/4  ( обозначения АВ=с , АС=b , ВС=а ) .

Рассм. ΔВСН, ∠ВНС=90° , ВН=ВК+НК=с/2+с/4=3с/4

Проведём КР⊥ВС  ⇒   ∠КРС=90° .

ΔКСН=ΔКСР , так как у этих прямоугольных треугольников имеется общая гипотенуза СК и равные острые углы ∠КСН=∠КСР  ⇒

КН=КР=с/4

В ΔВКР катет КР=с/4 , а гипотенуза ВК=с/2. То есть катет в 2 раза меньше гипотенузы, значит угол, лежащий против катета КР равен 30°  ⇒  ∠В=30° .

Из ΔВСН найдём  ∠ВСН=180°-∠ВНС-∠В=180°-90°-30°=60°

Так как ∠ВСН=∠ВСН+∠КСН , а ∠ВСН=∠КСН , то ∠ВСН=∠КСН=60°:2=30°   ⇒   ∠АСН=30°   ⇒   ∠АСВ=3*30°=90°

ΔАВС - прямоугольный

Радиус вписанной окружности в прямоугольный треугольник равен

$r=frac{a+b-c}{2}$

Так как в ΔАВС:  ∠В=30° , то АС=1/2*АВ , то есть   $b=frac{c}{2}; ; ,; ; c=2b$  .

$BC^2=AB^2-AC^2; ; ,; ; a^2=c^2-b^2=(2b)^2-b^2=3b^2; ; to ; ; a=bsqrt3\\r=frac{bsqrt3+b-2b}{2}=frac{(sqrt3-1)b}{2}$

Найдём площадь ΔАВС.

$S=frac{1}{2}cdot ab=frac{1}{2}cdot bsqrt3cdot b=frac{sqrt3b^2}{2}=1,5+sqrt3; ; Rightarrow \\b^2=frac{2(1,5+sqrt3)}{sqrt3}=frac{3+2sqrt3}{sqrt3}=sqrt3+2; ; ,; ; ; b=sqrt{2+sqrt3}\\r=frac{(sqrt3-1)sqrt{2+sqrt3}}{2}$

Answer 2

У меня описка, надо писать так: "Так как <ВСН=

Answer 3

угол ВСН=угол ВСК+угол КСН , а угол ВСК=углу КСН , то угол ВСК=уллу КСН=60:2=30 ...