Ответы
Ответ дал:
0
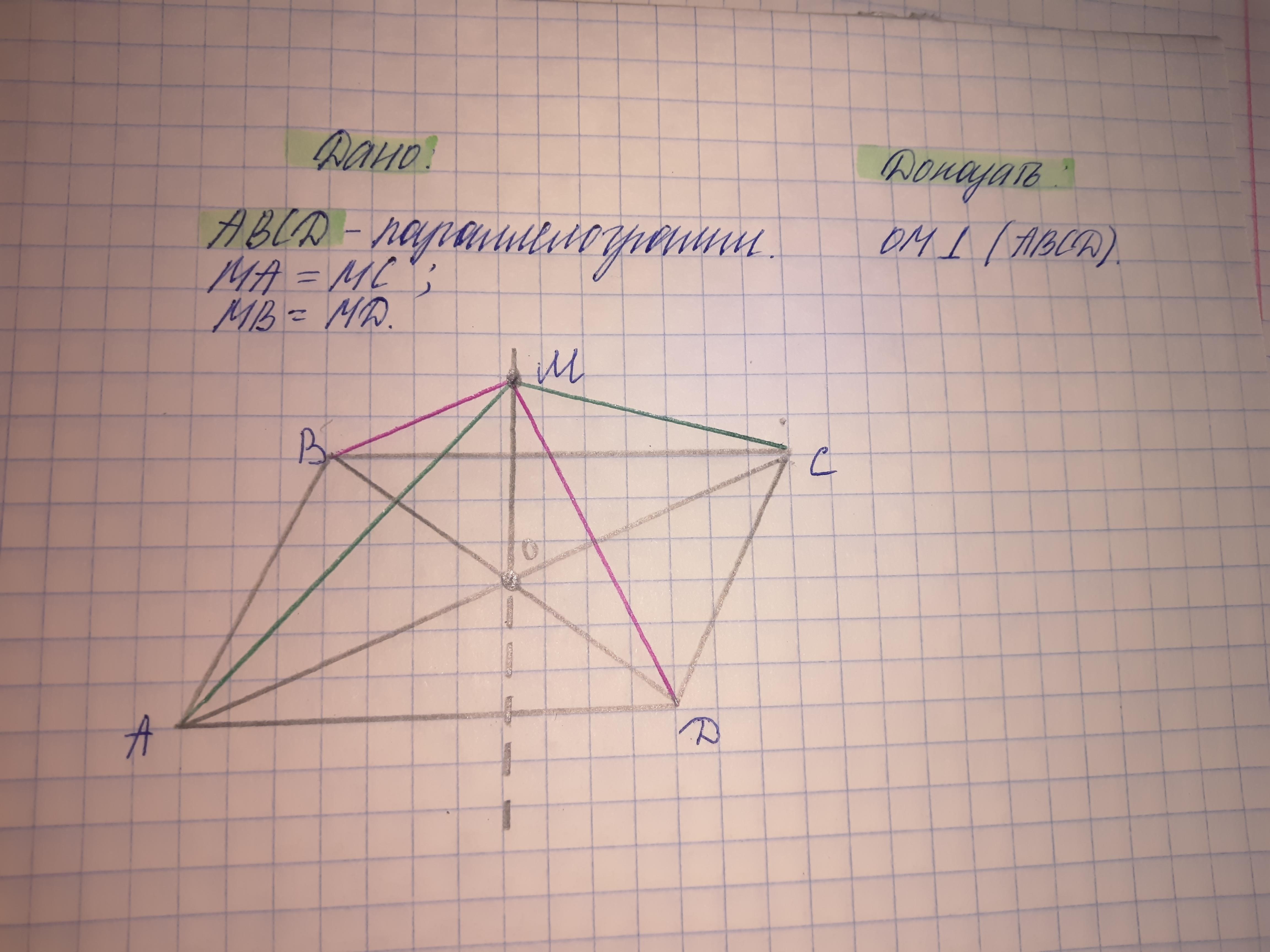
1.Т.к. АВСD - параллелограмм, то диагонали АС и ВD пересекаются и точкой пересечения делятся пополам, т.е. О-середина АС и середина ВD
2. Т.к. МА=МС, то ΔАМС - равнобедренный, в нем медиана ОМ является и высотой, т.к. проведена к основанию АС,
3. Совершенно аналогично т.к. ВО=DО, то в равнобедренном ΔВМD, а он равнобедренный, т.к. по условию МВ=МD, медиана ОМ является и высотой, т.к. проведена к основанию ВD
4. ОМ перпендикулярен двум пересекающимся прямым ВD и АС плоскости АВС, значит, ОМ перпендикулярен плоскости АВС по признаку перпендикулярности прямой и плоскости.
Требуемое доказано.
Вас заинтересует
3 года назад
3 года назад
8 лет назад
9 лет назад
9 лет назад