Ответы
Ответ дал:
0
пишу неравенство
надеюсь поможет
Приложения:


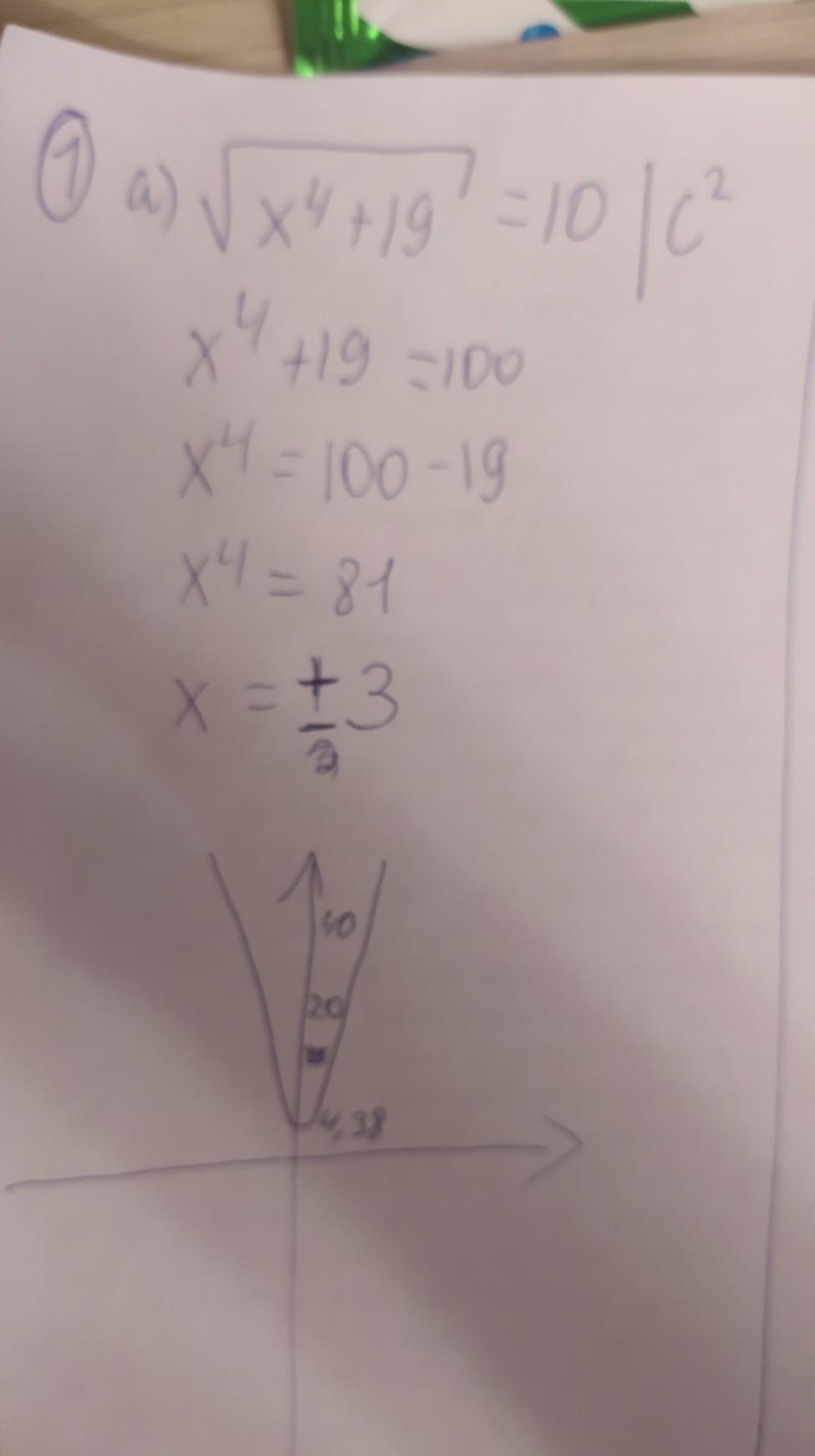
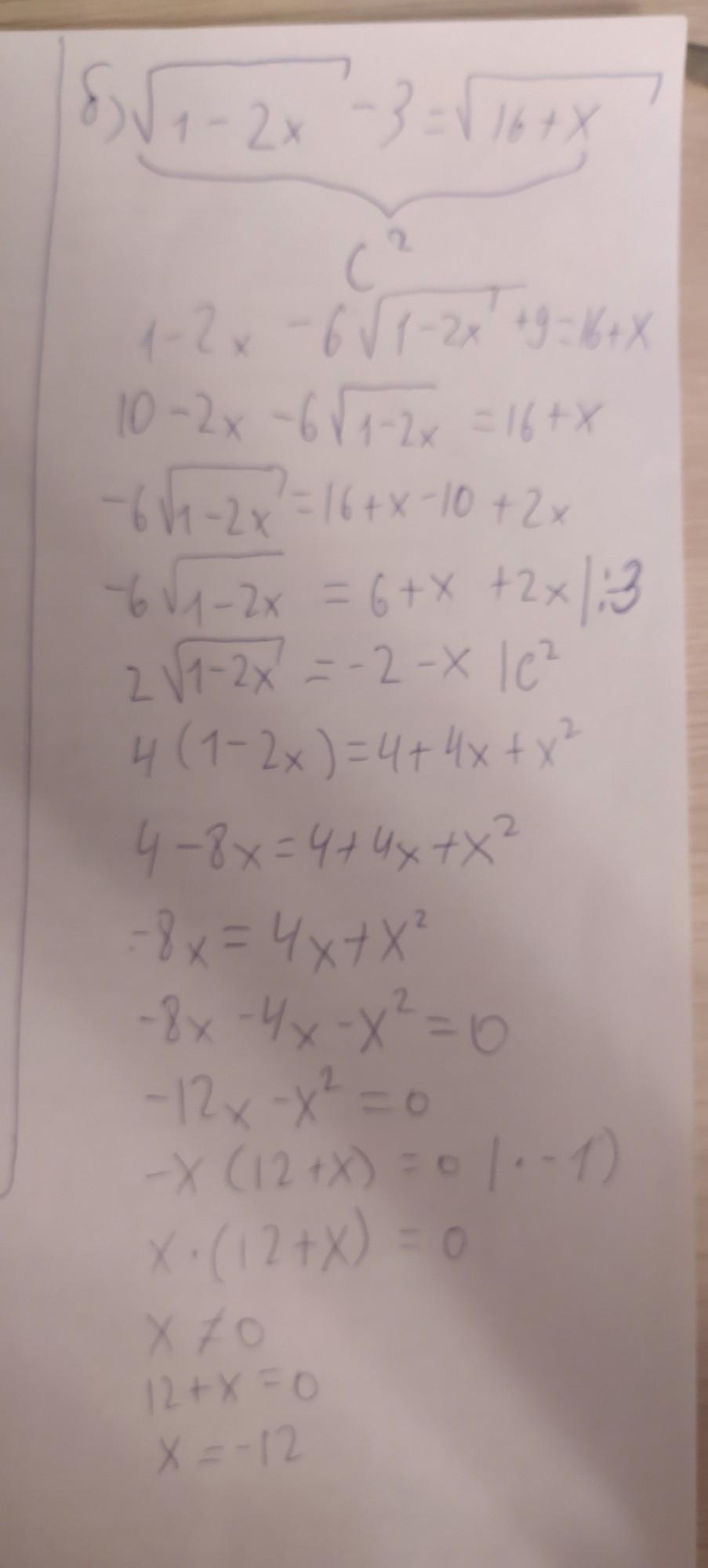
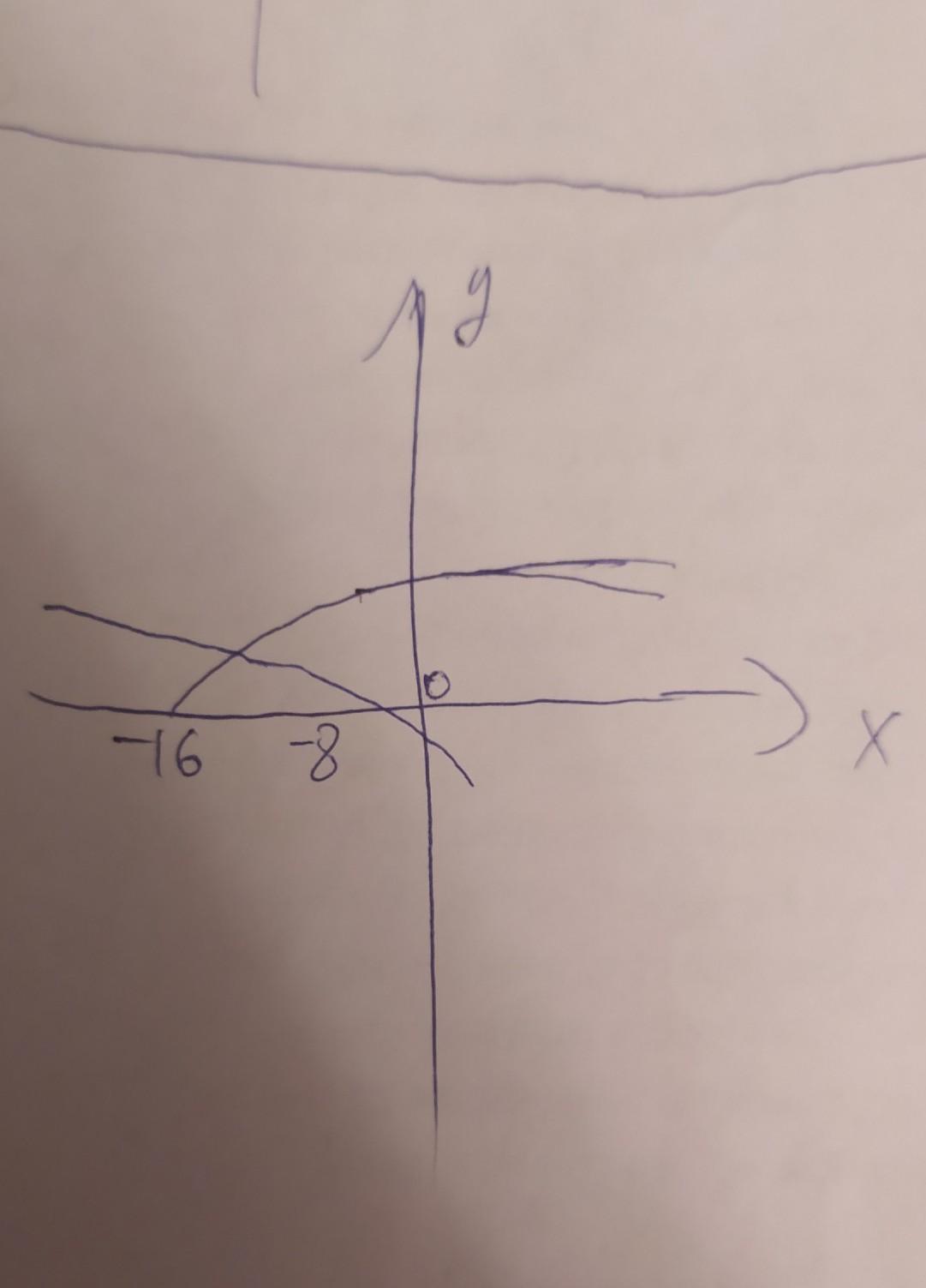
Ответ дал:
0
щас уравнения 1 решу
Ответ дал:
0
ок
Ответ дал:
0
#1.
a)
б)
#2.
Ответ:
#3.
a)
x ∈ (-11; 5]
б)
x ∈ [2,5; +∞)
Приложения:


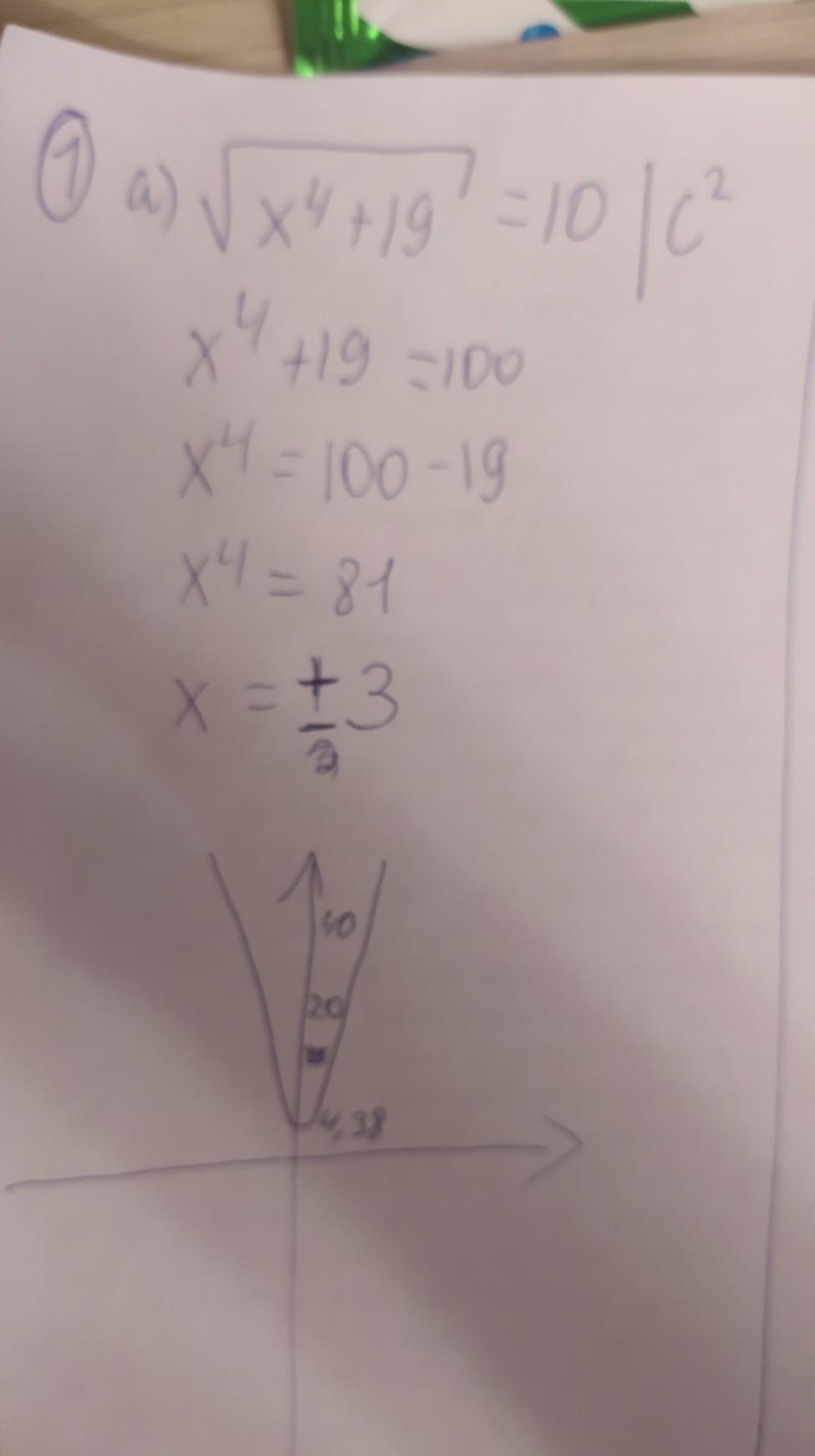
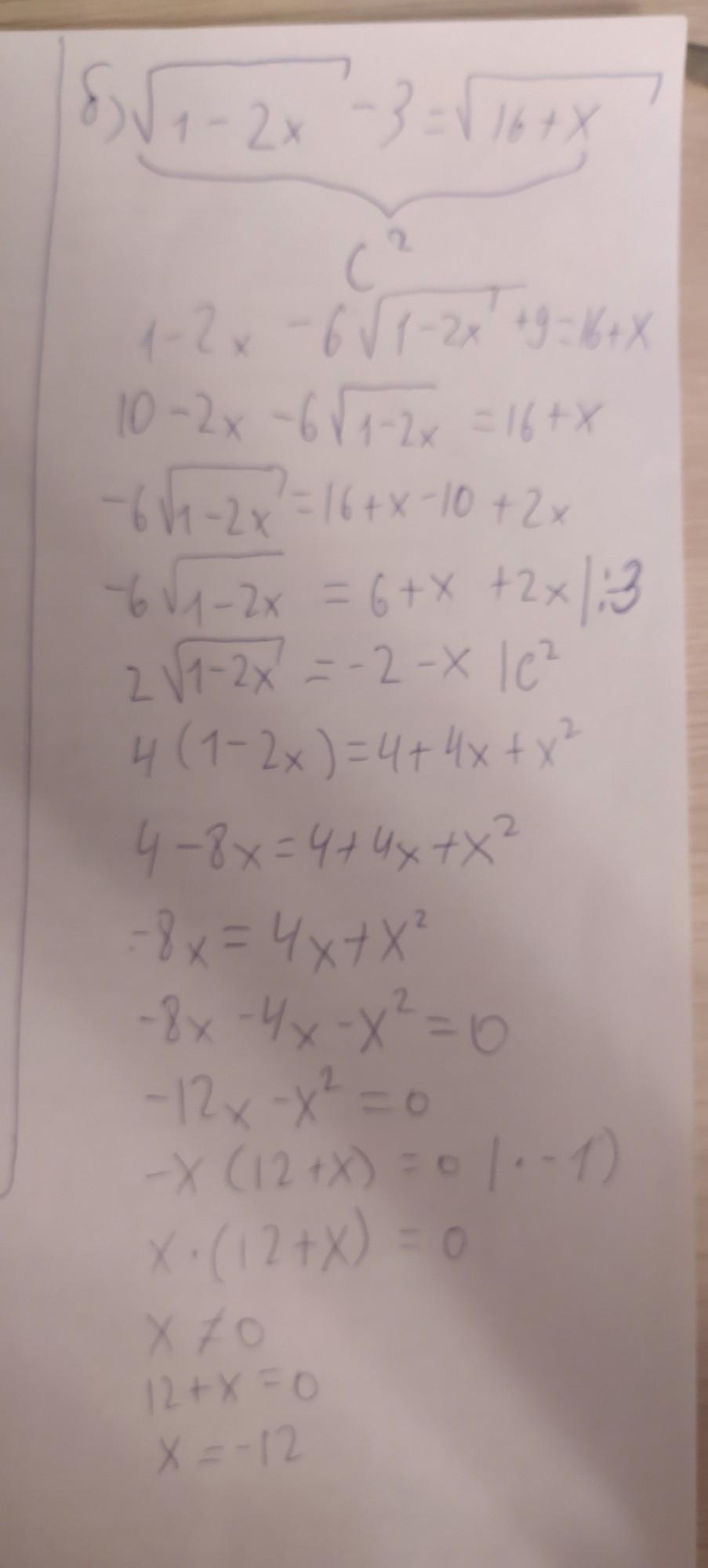
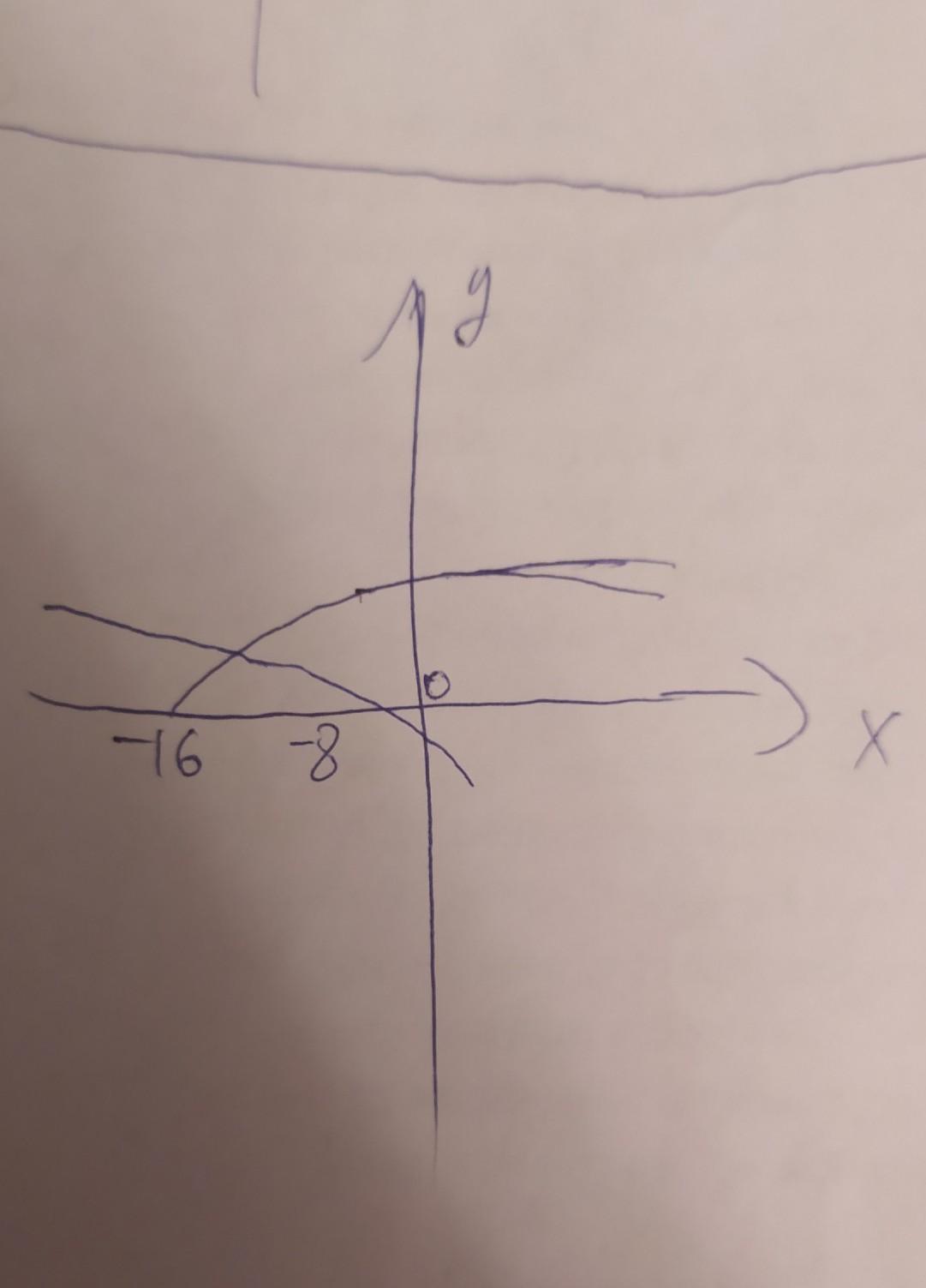
Ответ дал:
0
если интересно, то у меня в профиле ещё задание на 50 баллов есть, подобноеее
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад