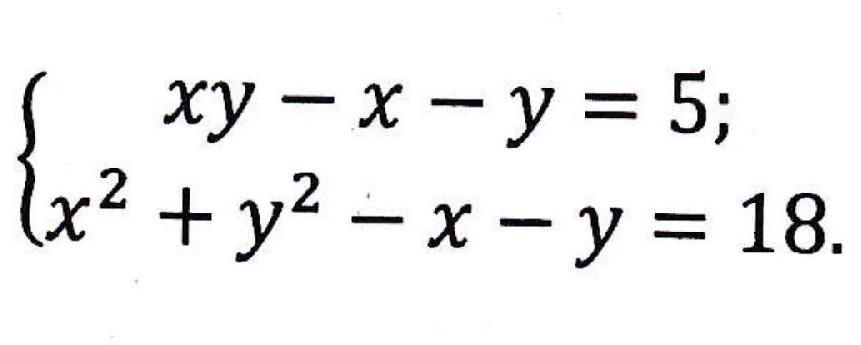Question

решите срочно очень надо​

Answer 1

Ответ:

$(3;4), (4;3), (-2+sqrt{3};-2-sqrt{3}), (-2-sqrt{3};-2+sqrt{3})$

Объяснение:

сделаем замену: x+y=t, тогда t²=(x+y)²=x²+2xy+y²

Выразим из первого уравнения системы xy:

xy=5+x+y

и применим нашу замену: xy=5+t, тогда

t²=x²+2xy+y²=x²+2(5+t)+y²

выразим x²+y²:

x²+y²=t²-2(5+t)=t²-10-2t

То есть, при решении данного примера делаем замену:

$left{begin{matrix}x+y=t\ xy=5+t \x^2+y^2=t^2-2t-10end{matrix}right.$

Применяем ко второму уравнению исходной системы:

$x^2+y^2-x-y=18 \ x^2+y^2-(x+y)=18\ \ t^2-2t-10-t=18 \ t^2-3t-28=0 \ t_1=7 \ t_2=-4$

Обратная замена (достаточно двух уравнений из системы выше):

$1) left{begin{matrix}x+y=7\ xy=5+7 end{matrix}right.Leftrightarrow left{begin{matrix}y=7-x\ xy=12 end{matrix}right. \ \ x(7-x)=12 \ 7x-x^2=12 \ x^2-7x+12=0 \x_1=3 \ x_2=4 \ \ y_1=7-x_1=7-3=4 \ y_2=7-x_2=7-4=3$

$2) left{begin{matrix}x+y=-4\ xy=5-4 end{matrix}right.Leftrightarrow left{begin{matrix}y=-4-x\ xy=1 end{matrix}right. \ \ x(-4-x)=1 \ -4x-x^2=1 \ x^2+4x+1=0 \ D=16-4=12 \ sqrt{D} =sqrt{12}=sqrt{4*3}=2sqrt{3} \ \ x_{3,4}=frac{-4^+_-2sqrt{3} }{2}=-2^+_-sqrt{3} \ \ y_{3,4}=-4-x=-4-(-2^+_-sqrt{3}) =-4+2^-_+sqrt{3} =-2^-_+sqrt{3}$