Question

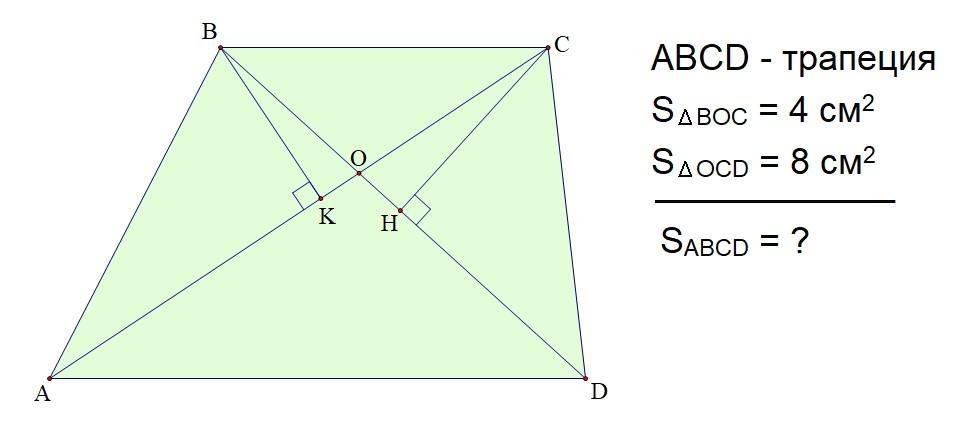
Дана трапеция ABCD(AD||BC), диагонали трапеции пересекаются в точке О. Sboc= 4 см², Scod= 8 см². Найдите площадь трапеции. ​

Answer 1

Ответ: 36 см²

Объяснение:

Площадь трапеции найдём как сумму площадей четырёх треугольников, образованных диагоналями.

1. Рассмотрим ΔBOC и ΔCOD.

Проведём из точки C перпендикуляр CH к стороне BD. Получим, что CH является высотой и ΔBOC, и ΔCOD. Выпишем формулы площади для этих треугольников:

$S_{Delta BOC}=frac{1}{2}CHcdot OB=4;cm^2\ \ S_{Delta COD}=frac{1}{2}CHcdot OD=8;cm^2$

Найдём частное этих площадей:

$frac{S_{Delta BOC}}{S_{Delta COD}}=frac{frac{1}{2}CHcdot OB}{frac{1}{2}CHcdot OD} =frac{OB}{OD} =frac{4}{8}=frac{1}{2} ;;Rightarrow;;frac{OB}{OD}=frac{1}{2}$

2. ∠BCA = ∠CAD (накрест лежащие углы при BC || AD и секущей AC)

∠CBD = ∠BDA (накрест лежащие углы при BC || AD и секущей BD)

3. Рассмотрим ΔBOC и ΔAOD:

1) ∠BCA = ∠CAD

2) ∠CBD = ∠BDA

Следовательно, ΔBOC и ΔAOD подобны по двум углам.

Причём k = OC : OA = OB : OD = 1/2  ⇒ OA = 2OC

4. Рассмотрим ΔBOC и ΔAOD. Отношение площадей подобных треугольников равно квадрату коэффициенту подобия. То есть:

$k^2=frac{1}{4} =frac{S_{Delta BOC}}{S_{Delta AOD}} ;;Rightarrow;;S_{Delta AOD}=4cdot S_{Delta BOC}=4cdot4=16;cm^2$

5. Рассмотрим ΔBOC и ΔABO.

Проведём из точки B перпендикуляр BK к стороне AC. Получим, что BK является высотой и ΔBOC, и ΔABO. Выпишем формулы площади для этих треугольников и преобразуем SΔABO:

$S_{Delta BOC}=frac{1}{2}BKcdot OC=4;cm^2\ \ S_{Delta ABO}=frac{1}{2}BKcdot OA=frac{1}{2}BKcdot 2OC=2cdot S_{Delta BOC}=2cdot4=8;cm^2$

6. Найдём площадь трапеции:

$S_{ABCD}=S_{Delta BOC}+S_{Delta AOD}+S_{Delta COD}+S_{Delta ABO}=4+16+8+8=36;cm^2$