Question

Высота правильной четырехугольной пирамиды равна 6√3 см, а боковое ребро наклонено к плоскости основания под углом 60º.
• найдите боковое ребро пирамиды.
• найдите площадь боковой поверхности пирамиды.
Подробно

Answer 1

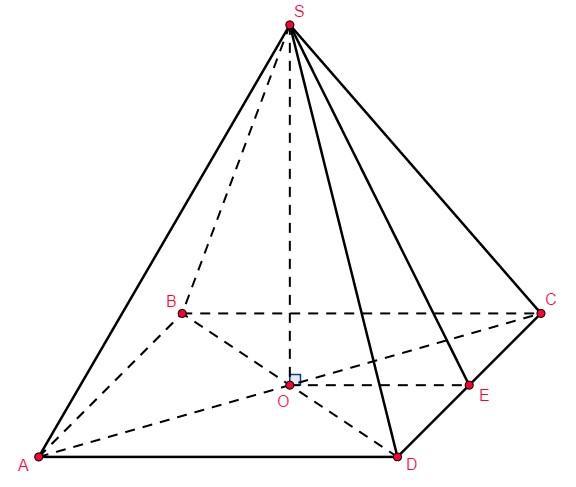
Поскольку четырехугольная пирамида правильная, то в её основании служит квадрат. По условию, $SO=6sqrt{3}$ см и $angle ODS=60^circ$.

Найдём боковое ребро пирамиды из прямоугольного треугольника $SOD$, т.е. $sin angle 60^circ =dfrac{SO}{SD}~~Rightarrow~~ SD=dfrac{6sqrt{3}}{dfrac{sqrt{3}}{2}}=12~_{sf cm}$

$angle OSD=90^circ -angle ODS=30^circ$ . Против угла 30° катет в два раза меньше гипотенузы, т.е. $OD=dfrac{SD}{2}=6$ см. Тогда $BD=2OD=12$ см.

$AD=dfrac{BD}{sqrt{2}}=dfrac{12}{sqrt{2}}=6sqrt{2}$ см

OE - радиус вписанной окружности: OE = AD/2 = 3√2 см.

Найдем апофему SE: $SE=sqrt{9cdot 2+36cdot 3}=sqrt{126}=3sqrt{14}$ см.

$S_{bok}=dfrac{1}{2}P_ocdot SE=dfrac{1}{2}cdot 4cdot 6sqrt{2}cdot 3sqrt{14}=72sqrt{7}$ см²

Answer 2

Изучайте давай. У меня нет нужды ради вас переписывать.

Answer 3

Всё как написано )