Question

Задание на фотографии

Answer 1

Найти массу тела, ограниченного цилиндрической поверхностью  x²=2y и плоскостями  x+z=1 ,  2y+z=2 , если в каждой его точке объёмная плотность численно равна ординате этой точки.

=========================================

m = ρ·V  , где  m - масса тела,  V - объём тела,

               ρ (x, y, z) = y    - объёмная плотность по условию

$boldsymbol{m = iiintlimits_V {rho(x,y,z) } dx dy dz = iiintlimits_V {y} dx dy dz}$

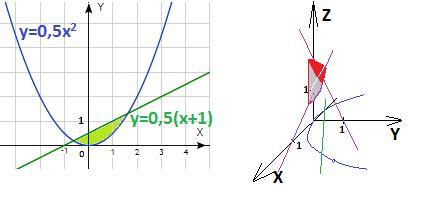
Проекция цилиндрической поверхности  x²=2y  на плоскость  xOy - парабола  y=0,5x². Ограничена по y≥0 снизу, но не ограничена сверху.

x+z=1,  2y+z=2  - уравнения плоскостей. Для нахождения проекции линии их пересечения на плоскость xOy составим систему

$displaystyleleft { {{2y+z=2} atop {x+z=1}} right. -\\~~~2y-x=1 Rightarrow y=dfrac{x+1}2$  

0 ≤ y ≤ 0,5(x + 1)     -  границы интегрирования по у

Точки пересечения параболы y=0,5x²  и прямой y=0,5(x+1)  на плоскости xOy

$0,5x^2=0,5(x+1) big|cdot 2\x^2=x+1\x^2-x-1=0\D=1+4=5 x_{1,2}=dfrac{1pmsqrt5}2\\boldsymbol{dfrac{1-sqrt5}2leq xleq dfrac{1+sqrt5}2}$

                     - границы интегрирования по х

Осталось определить, какая из плоскостей по z лежит ниже. Для этого достаточно подставить координаты  вершины параболы  для нахождения аппликаты точек пересечения плоскостей с цилиндрической поверхностью.

x = 0;  y = 0

x + z = 1;    0 + z = 1;   z = 1   -   (0;0;1) -  точка плоскости  z=1-x  

2y + z = 2;    2·0 + z = 2;   z = 2  - (0;0;2)   -  точка плоскости  z=2-2y

1 - x ≤ z ≤ 2 - 2y  -  границы интегрирования по z

$displaystyle m = iiintlimits_V {y} dx dy dz=intlimits^frac{1+sqrt5}2_frac{1-sqrt5}2dx intlimits^frac{x+1}2}_0y dyintlimits^{2-2y}_{1-x}dz\\intlimits^{2-2y}_{1-x}dz=zbigg|^{2-2y}_{1-x}=2-2y-1+x=x-2y+1\\intlimits^frac{x+1}2}_0y(x-2y+1) dy=intlimits^frac{x+1}2}_0big(xy-2y^2+ybig) dy=\\=dfrac{xy^2}2-dfrac{2y^3}3+dfrac {y^2}2bigg|^{frac{x+1}2}_0=y^2Bigg(dfrac{x}2-dfrac{2y}3+dfrac 12Bigg)bigg|^{frac{x+1}2}_0=$

$=Bigg(dfrac{x+1}2Bigg)^2cdot Bigg(dfrac{x}2-dfrac{2(x+1)}6+dfrac 12Bigg)-0=\\=dfrac{(x+1)^2}4cdot Bigg(dfrac{3x-2x-2+3}6Bigg)=dfrac{(x+1)^3}{24}$

$displaystyleintlimits^frac{1+sqrt5}2_frac{1-sqrt5}2dfrac{(x+1)^3}{24} dx=dfrac 1{24}cdot intlimits^frac{1+sqrt5}2_frac{1-sqrt5}2(x+1)^3 d(x+1)=\\\=dfrac 1{24}cdotdfrac{(x+1)^4}4bigg|^frac{1+sqrt5}2_frac{1-sqrt5}2=dfrac 1{96}cdot(x+1)^4bigg|^frac{1+sqrt5}2_frac{1-sqrt5}2=\\\=dfrac 1{96}cdotBigg(bigg(dfrac{1+sqrt5}2+1bigg)^4-bigg(dfrac{1-sqrt5}2+1bigg)^4Bigg)=\\=dfrac 1{96}cdotBigg(bigg(dfrac{3+sqrt5}2bigg)^4-bigg(dfrac{3-sqrt5}2bigg)^4Bigg)=$

$=dfrac1{96}cdot dfrac 1{16}cdot bigg(Big(3+sqrt5}Big)^4-Big(3-sqrt5}Big)^4bigg)=\\=dfrac1{1536}cdot bigg(Big(3+sqrt5}Big)^2+Big(3-sqrt5}Big)^2bigg)bigg(Big(3+sqrt5}Big)^2-Big(3-sqrt5}Big)^2bigg)=\\=dfrac1{1536}cdot 28cdotbigg(3+sqrt5+3-sqrt5bigg)bigg(3+sqrt5-3+sqrt5bigg)=\\=dfrac7{384}cdot6cdot2sqrt5=dfrac{7sqrt5}{32}$

$\\boxed{boldsymbol{m=dfrac{7sqrt5}{32}approx 0,489}}$

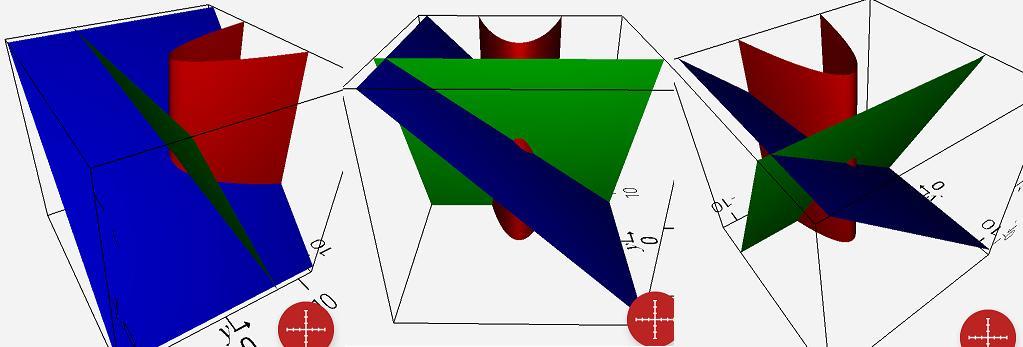
Во втором приложении разные ракурсы полученной объёмной фигуры.