Ответы
Ответ дал:
0
Ответ:
АC = BC
Объяснение:
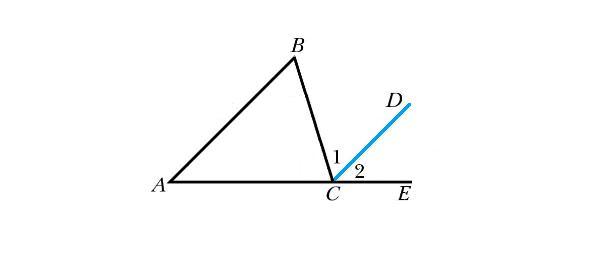
1) AB||CD, BC - секущая, ∠1 и ∠ABC - накрест лежащие углы. Согласно признаку, если две параллельные прямые пересечены секущей, то накрест лежащие углы равны, делаем вывод что ∠1 = ∠ABC. 2) AB||CD, AC - секущая, ∠2 и ∠BAC - соответственные углы. Согласно признаку, если две параллельные прямые пересечены секущей, то соответственные углы равны, делаем вывод что ∠2 = ∠BAC. 3) Из дано известно, что ∠1 = ∠2 ⇒ ∠ABC = ∠BAC. Согласно свойству, если в треугольнике два угла равны, то треугольник равнобедренный. ⇒ ΔABC - равнобедренный. ⇒ AC = BC.
Вас заинтересует
2 года назад
3 года назад
3 года назад
10 лет назад