Question

ПОМОГИТЕ ПОЖАЛУЙСТА, ДАМ 70 БАЛЛОВ

Answer 1

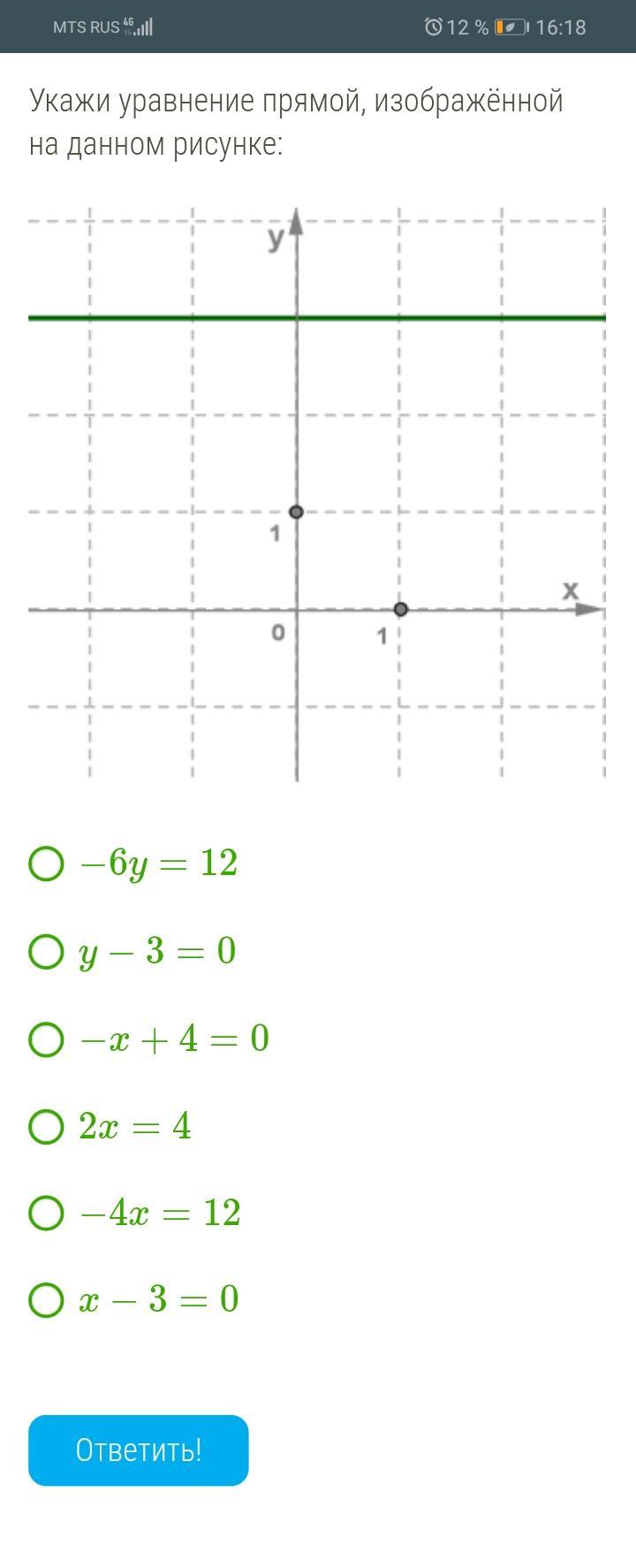
Первый способ

Частным случаем линейной функции $y = kx + b$ является случай, когда $k = 0$ и эта функция приобретает вид $y = b$. Графиком данной функции является прямая, параллельная оси абсцисс (оси $x$).

Из предложенного графика видно, что ордината $y$ при всех значениях независимой переменной $x$ равна $3$, следовательно $y = 3$, или $y - 3 = 0$.

Второй способ

Предложенным графиком является прямая, значит, функция является линейной вида $y = kx + b$, где $k$ и $b$ — некоторые числа (коэффициенты).

Как известно, для построения прямой достаточно двух точек. Возьмем точки из графика, например $(1; 3)$ и $(2; 3)$, и подставим их координаты в уравнение функции. Получили систему линейных уравнений с двумя переменными:

$displaystyle left { {{3 = k + b } atop {3 = 2k + b}} right.$

$k + b = 2k + b\k = 0$

Тогда $3 = 0 + b; b = 3$

Таким образом, $y = 3$, или $y - 3 = 0$, — искомое уравнение прямой

Ответ: $y - 3 = 0$