Question

В прямоугольном параллелепипеде длина диагонали основания равна 5 см, а косинус угла, который она составляет с большей стороной нижнего основания, равен 0,8. Через эту и противоположную ей сторону верхнего основания проведена плоскость, косинус угла наклона которой к плоскости нижнего основания равен 0,3. Найти площадь этого сечения.

Answer 1

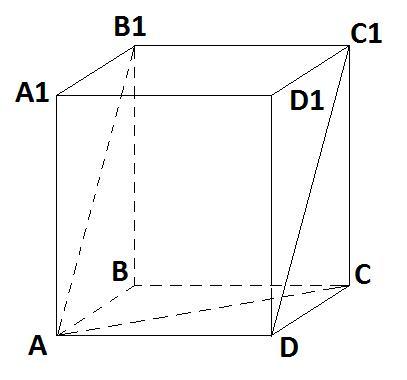
$ABCDA_1B_1C_1D_1$ - прямоугольный параллелепипед.

$AC=5$ см

$cosangle CAD=0,8\cosangle CDC_1=0,3$

Найти $S_{AB_1C_1D}$

Решение:

Из треугольника ACD:

$cosangle CAD=frac{AD}{AC}Rightarrow AD=ACcdotcosangle CAD=5cdot0,8=4$ см

По т.Пифагора

$AC^2=AD^2+CD^2Rightarrow CD=sqrt{AC^2-AD^2}=sqrt{25-16}=sqrt9=3$ см

Из треугольника CC1D:

$cosangle CDC_1=frac{CD}{C_1D}Rightarrow C_1D=frac{CD}{cosangle CDC_1}=frac{3}{0,3}=10$ см

Площадь сечения

$S_{AB_1C_1D}=ADcdot C_1D=4cdot10=40$ см²