Помогите решить в,г,д.
Кому не сложно можете написать РАЗБОРЧИВЫМ почерком все объяснения ( полное решение)
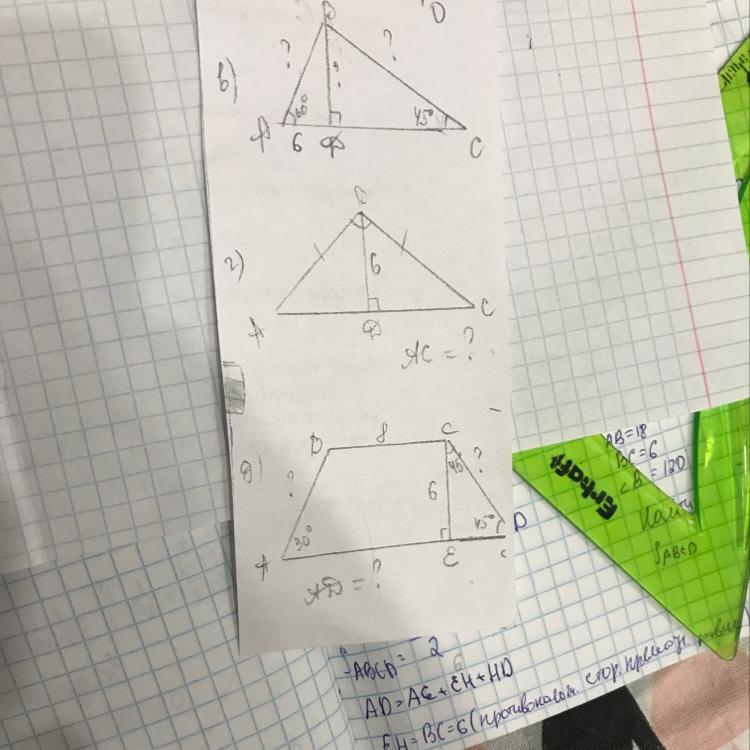
Ответы
в)
Р-м ΔADB:
ΔADB — прямоугольный, ∠ABD = 180−(90+60) = 30°.
Найдем неизвестные стороны через синусы углов:
ΔCDB — прямоугольный (и равнобедренный), ∠CBD = 180−(90+45) = 45°.
Найдем гипотенузу BC через синус угла:
Ответ: AB = 12, BD = 6√3, BC = 6√6.
г)
Р-м ΔABC:
ΔABC — прямоугольный (∠B = 90°), равнобедренный (AB = BC) ⇒ ∠A = ∠C = (180−90)/2 = 45°
Р-м ΔADB:
∠ABD = 180−(90+45) = 45° ⇒ ΔADB — равнобедренный ⇒ AD = BD = 6.
С ΔCDB — аналогично как с ΔADB ⇒ DC = BD = 6.
AC = AD+DC = 6+6 = 12.
Ответ: AC = 12.
д)
Опустим вторую высоту BH на основу AD. HE = DC = 8 с, т.к HBCE — прямоугольник.
Р-м ΔCED:
ΔCED — прямоугольный (∠CED = 90°), равнобедренный. CE = ED = 6. Найдем гипотенузу через синус угла:
Р-м ΔABH:
ΔABH — прямоугольный (∠AHB = 90°). Найдем гипотенузу через синус угла.
Найдем оставшийся катет через AH через тангенс угла:
AD = AH+HE+ED = 6√3+8+6 = 14+6√3 ≈ 24.4
Ответ: AD = 24.4, AB = 12, CD = 6√2.