Question

Очень нужна помощь!5 заданий. и алгебра и геометрия​

Answer 1

$1.\log_6(x+1)+log_6(2x+1)leq1\log_6left((x+1)(2x+1)right)leq1\log_6(2x^2+3x+1)leq1\2x^2+3x+1leq1\2x^2+3xleq0\x(2x+3)leq0\boxed{xin[-1,5;;0]}\\2.\2sin^2x=1+cos x\2cdot(1-cos^2x)=1+cos x\2-2cos^2x-1-cos x=0\2cos^2x+cos x-1=0\cos x=t,;cos^2x=t^2,;tin[-1;;1]\2t^2+t-1=0\D=1-4cdot2cdot(-1)=1+8=9\t_{1,2}=frac{-1pm3}4\t_1=-2;-;He;nogx.\t_2=frac12\cos x=frac12Rightarrowboxed{x=pmfracpi3+2pi n,;ninmathbb{Z}}$

$3.\begin{cases}5-4x-x^2geq0\x+2neq0end{cases}Rightarrowbegin{cases}x^2+4x-5leq0\xneq-2end{cases}Rightarrowbegin{cases}(x+5)(x-1)leq0\xneq-2end{cases}Rightarrow\\\Rightarrowboxed{xin[-5;;-2)cup(-2;;1]}$

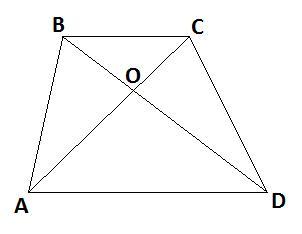
4. (см. рис.)

ABCD - трапеция, BD = 28 см, AO = 5 см, CO = 9 см.

Решение:

∠CBD = ∠BDA как накрест лежащие при AD║BC и секущей BD

∠BCA = ∠CAD как накрест лежащие при AD║BC и секущей AC.

Треугольники AOD и BOC подобны по первому признаку.

5:9 - коэффициент подобия.

5+9 = 14

28:14 = 2 см

2·5 = 10 см BO

2·9 = 18 см DO