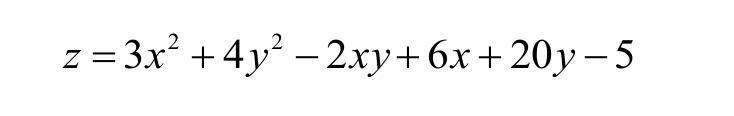Ответы
Ответ дал:
0
Ответ:
z(-2;-3)=-41 - минимум функции
Пошаговое объяснение:
M(-2;-3) - стационарная точка
M(-2;-3) - точка минимума
Ответ дал:
0
Спасииииибо !)
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
9 лет назад
9 лет назад