Question

Дана функция f(x) = x^3/3 - 9x - 7
а) Промежутки возрастания и убывания
б) её точки максимума и минимума

Answer 1

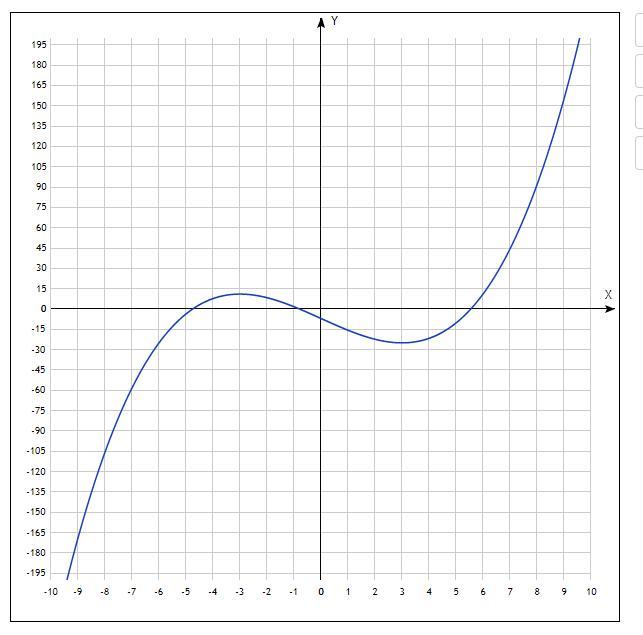
Ответ: а) промежутки возрастания: (-беск, -3) и (3, беск), промежуток убывания (-3, 3). Точка максимума: x = -3, Точка минимума: x = 3.

Пошаговое объяснение:Ищем первую производную: f'(x) = x^2 - 9 = (x-3)(x+3)

Нули производной: f'(x) = 0 = (x - 3)(x + 3); x = 3 или x = -3.

Проверим три промежутка: (-беск, -3), (-3, 3) и (3, беск)

1. (-беск, -3): f'(-5) = 16 - функция возрастает.

2. (-3, 3): f'(0) = -9, функция убывает.

3. (3, беск): f'(5) = 16 - функция возрастает.

Точка максимума: x = -3

Точка минимума: x = 3

Снизу график функции, подтверждающий строки сверху