Question

СРОЧНО ПОМОГИТЕ ПОЖАЛУЙСТА

найти площадь фигуры ограниченной данными линиями

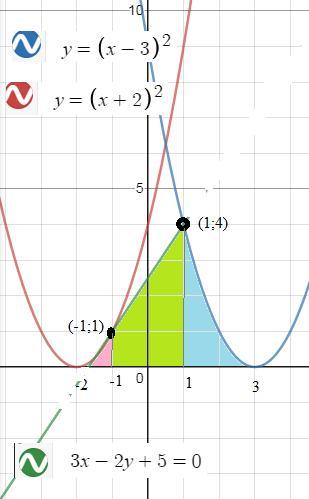
1)параболами у=(х+2)^2 , у=(х-3)^2 , осью Ох и прямой, проходящей через точки (-1;1) и (1;4)

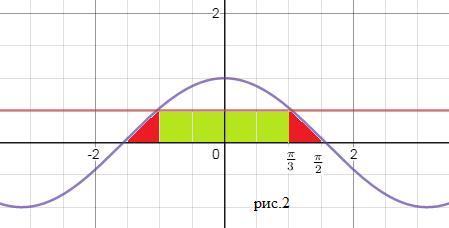
2)графиком функции у=соs x , прямой у=1/2 и отрезком [-п/2;п/2] оси Ох

Answer 1

Скорее всего прямая только соединяет точки (-1;1) и (1;4)

Тогда фигура, состоит из трех частей см рис.1

$S=intlimits^{-1}_{-2} {(x+2)^2} , dx +intlimits^{1} _{-1} {frac{3x+5}{2} } , dx +intlimits^3_1 {(x-3)^2} , dx =\\=frac{(x+2)^3}{3}|^{-1}_{-2}+(frac{3x^2}{4}+frac{5}{2}x)|^{1}_{-1}+frac{(x-3)^3}{3}|^{3}_{1}=frac{1}{3}+5+frac{8}{3}=8$

2)

cм. рис. 2

Фигура симметрична относительно оси Оу, поэтому можно считать половину площади на [0;π/2]

$S=2cdot(frac{pi }{3}cdot frac{1}{2}+intlimits^{frac{pi }{2} }_{frac{pi }{3} } {cosx} , dx )=frac{pi }{3}+2(-sinx)| ^{frac{pi }{2} }_{frac{pi }{3} }=frac{pi }{3}+2(-sinfrac{pi }{2}+sinfrac{pi }{3} )=frac{pi }{3} -2+sqrt{3}$