Question

.
Дано:
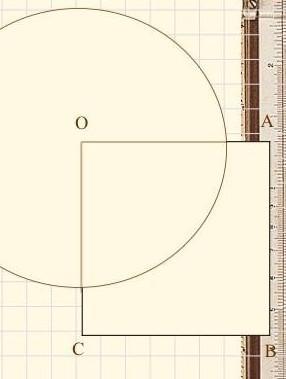
ОАВС-квадрат
AB = 6 см
Окружность с центром
О радиуса 5 см
Найти:
секущие из прямых ОА,
AB, BC, AC​

Answer 1

Ответ:

Дано:

Оавс-квадрат

ОА=6см; r=5см

Решение: Секущая= АС

Диагональ ОВ -| ОА^2+ ОС^2= | 36-36 = 6| 2

Половина диагонали ОВ=3| 2 или 4,24, что меньше радиуса 5 см

Стороны ОА и ОС больше радиуса и не могут называться секущей т к пересекают окружность в одной точке, а у секущей две точки пересечения.

Answer 2

спасибо))