Ответы
Ответ дал:
0
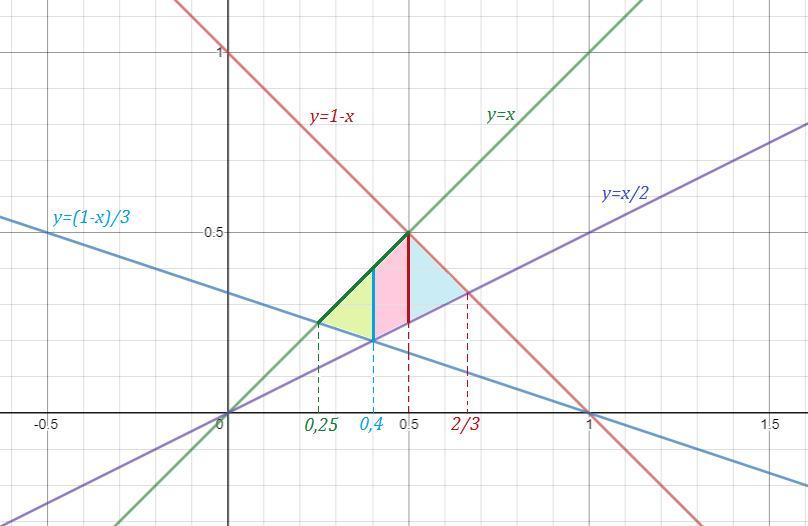
Область ограничена прямыми .
Найдём точки пересечения и разобьём область на сумму простейших областей.
Приложения:
Ответ дал:
0
Спасибо большое.
Ответ дал:
0
Ответ:
с помощью интегралов, если в вычислениях не ошибся
Пошаговое объяснение:
Приложения:

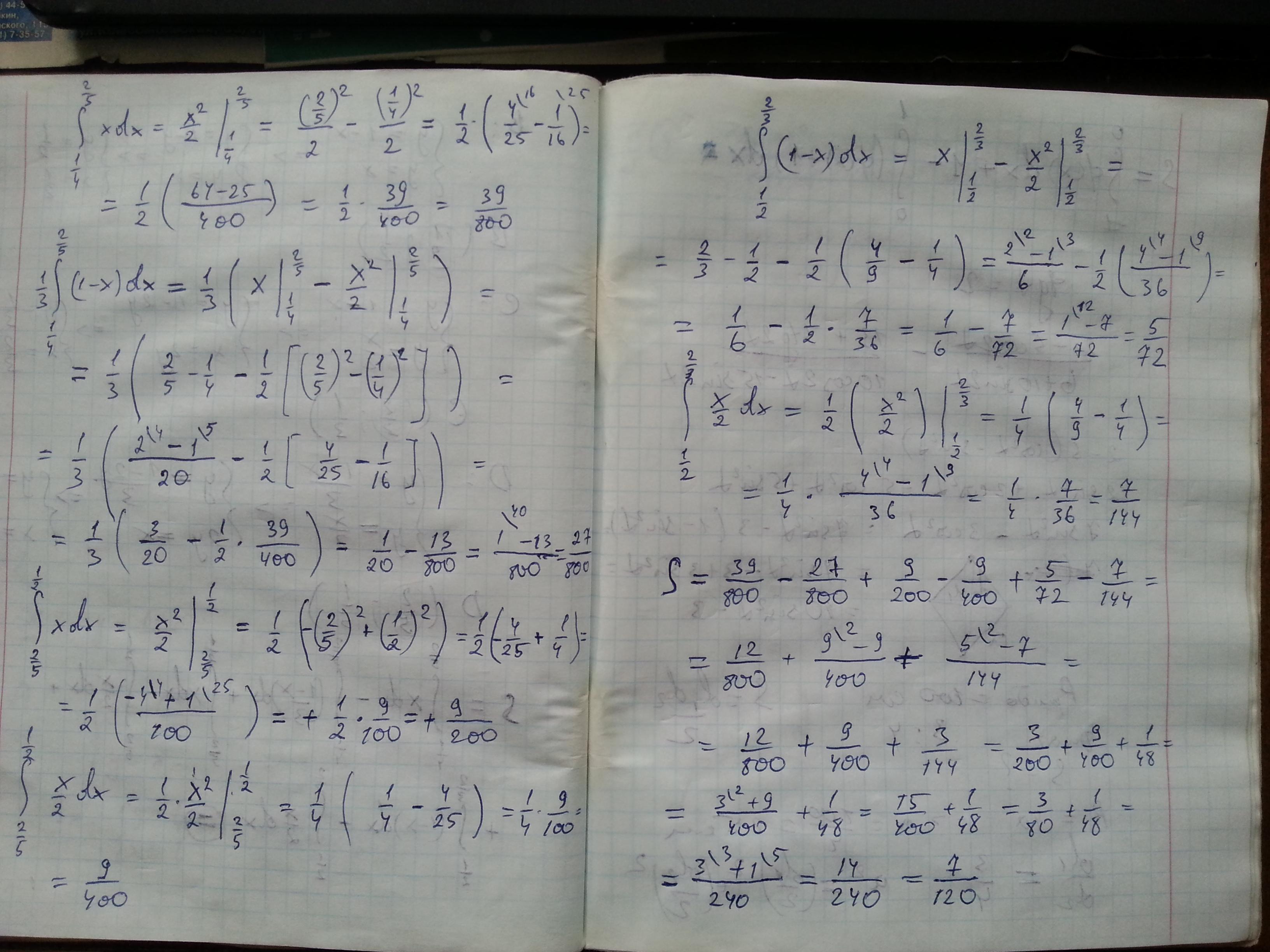
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад