Question

Нужно найти х . Все данные на рисунке​

Answer 1

Задача:

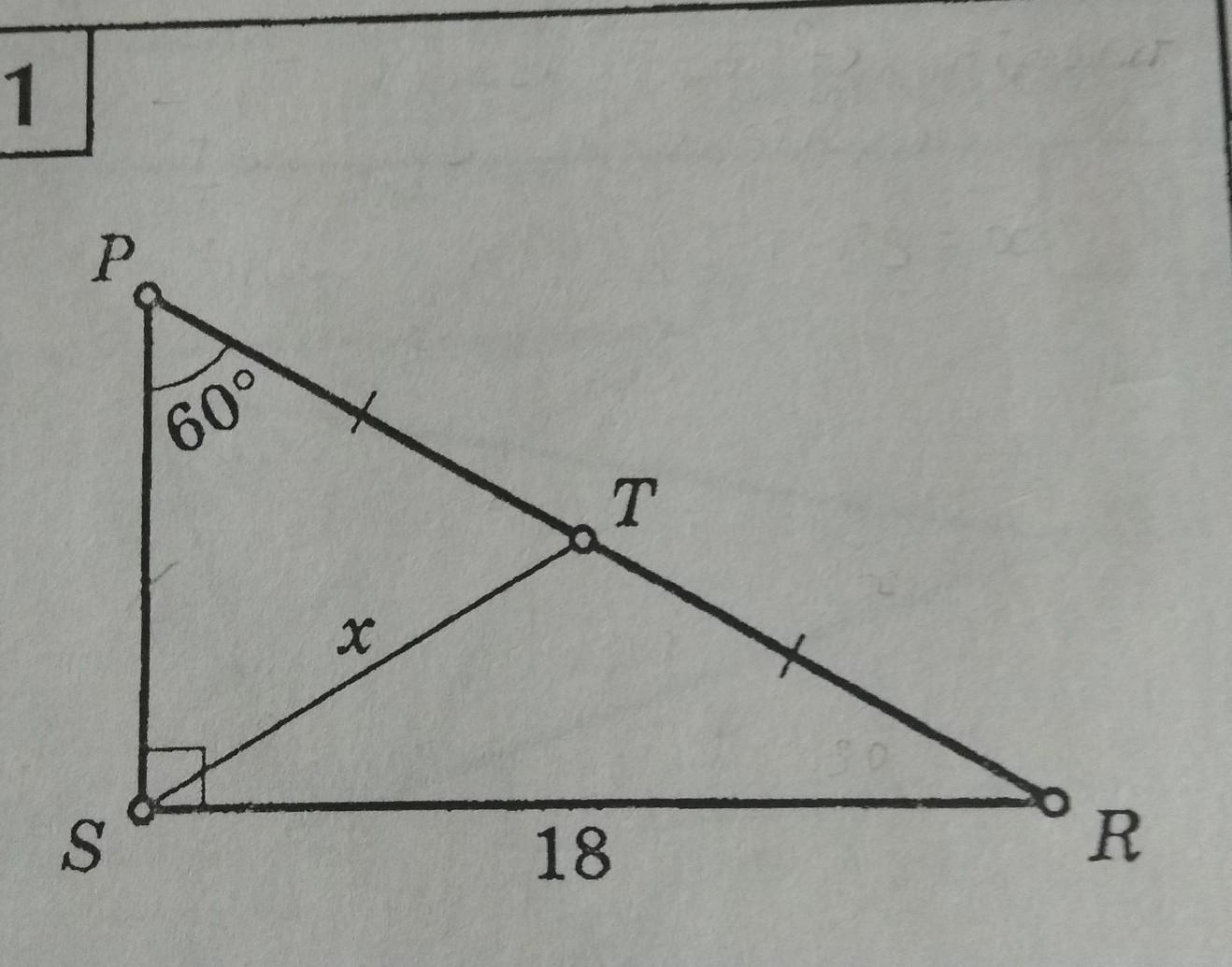
Дан прямоугольный треугольник SRP, ∠S = 90°, ∠P = 60°, PT = TR, SR = 18, ST — x.

Решение:

PR — гипотенуза прямойгольного Δ PRS. ST (x) — отрезок, проведенный из вершины S к PR.

PT = TR ⇒ ST — медиана.

Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.

Следовательно, найдем гипотенузу RP, найдем и медиану ST (x).

Воспользуемся формулой синуса угла:

$sin60^o=frac{SR}{PR} => PR = frac{SR}{sin60^o} \PR = frac{18}{frac{sqrt{3} }{2}} = frac{18 cdot 2}{sqrt{3} } =frac{36 cdot sqrt{3}}{sqrt{3}cdot sqrt{3}} =frac{36 cdot sqrt{3}}{3} = 12sqrt{3}$

ST = (12√3)/2 = 6√3.

Ответ:

x = 6√3

Answer 2

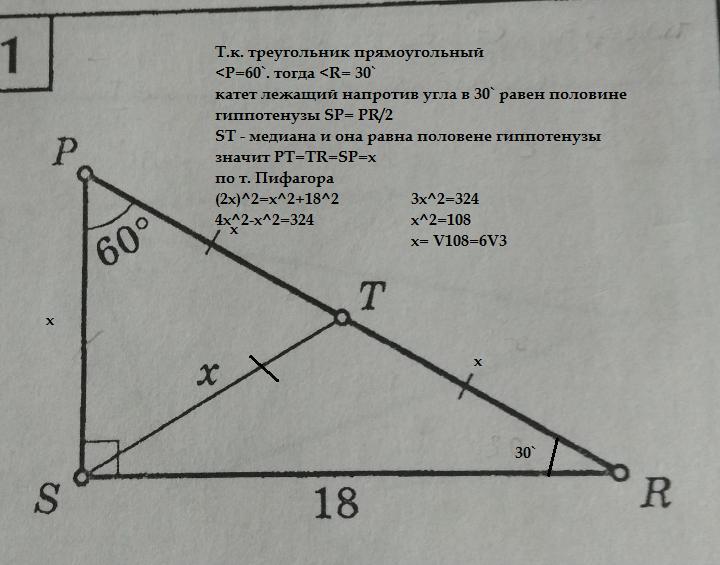
Решение на картинке _______

Answer 3

нужно было просто догадаться, если там х, значит искать через отношение