Тригонометрия, 9 класс.
Со всеми решениями, пожалуйста.
Вариант Б2. Буквы б в номерах 1 и 2
Приложения:
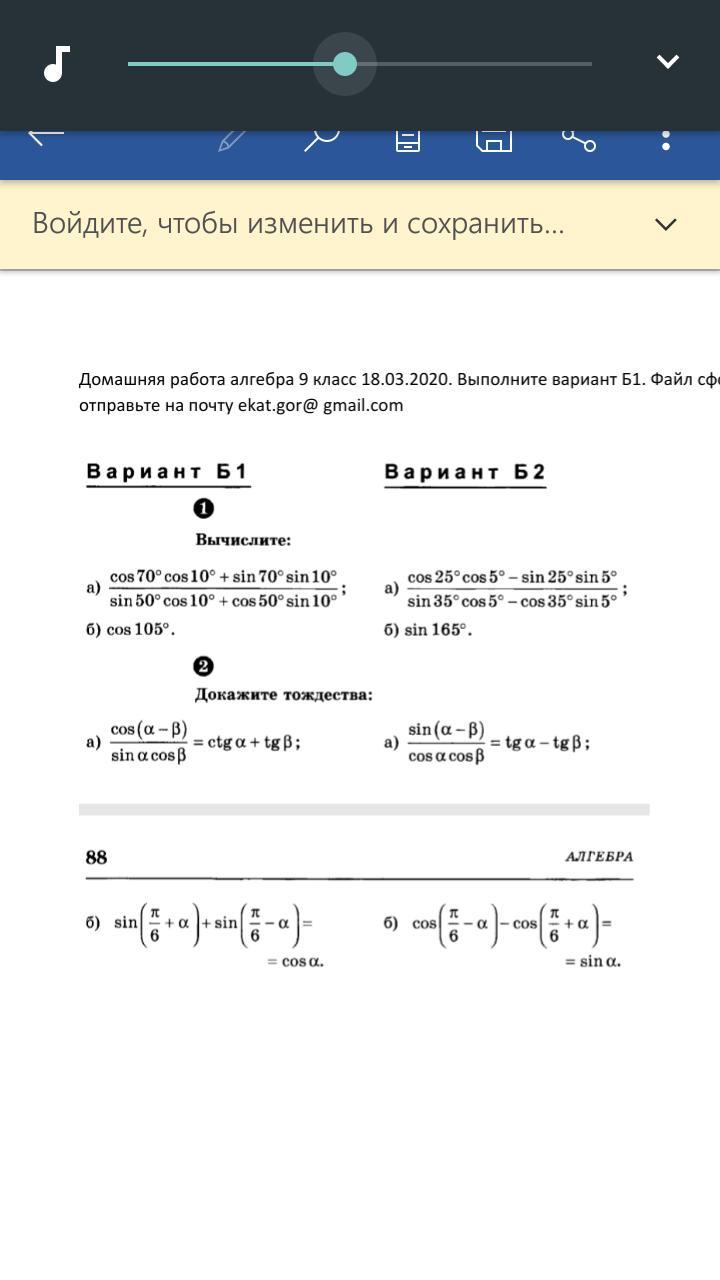
Ответы
Ответ дал:
0
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад