Question

Решить дифференциальное уравнение...

Answer 1

$(y+x)y'=-y\ underbrace{y}_{P(x,y)}dx+underbrace{(y+x)}_{Q(x,y)}dy=0\ P'_y=1,;;;Q'_x=1=>P'_y=Q'_x$

А значит имеем уравнение в полных дифференциалах, т.е.

$exists F(x,y): F'_x=P(x,y), F'_y=Q(x,y)\ F=int Pdx +phi_1(y)=int ydx+phi_1(y)=xy+phi(y)\ y+x=(xy+phi(y))'_y=>y+x=x+phi'_y=>phi '_y=y=>phi = dfrac{y^2}{2}+C_1\ xy+dfrac{y^2}{2}+C_1=0\ __________________________________$

$xy+dfrac{y^2}{2}+C_1=0,; y(0)=1\ dfrac{1}{2}+C_1=0=>C-1=-dfrac{1}{2}\ xy+dfrac{y^2}{2}-dfrac{1}{2}=0\ y^2+2xy-1=0\ y=dfrac{-2xpmsqrt{4x^2+4}}{2}=-xpmsqrt{x^2+1}$

При этом из двух полученных уравнений лишь одна кривая $y=-x+sqrt{x^2+1}$ проходит через указанную точку.

__________________________________________________

$y'=-1+dfrac{2x}{2sqrt{x^2+1}}=-1+dfrac{x}{sqrt{x^2+1}}<-1+dfrac{sqrt{x^2+1}}{sqrt{x^2+1}}=-1+1=0$

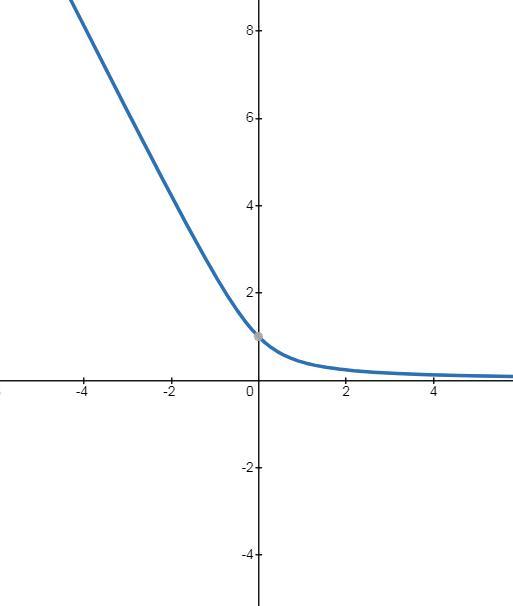
А значит искомая кривая монотонно убывает

$y''=dfrac{sqrt{x^2+1}-x*frac{x}{sqrt{x^2+1}}}{x^2+1}=dfrac{x^2+1-x^2}{(x^2+1)sqrt{x^2+1}}=dfrac{1}{(x^2+1)sqrt{x^2+1}}>0$

А тогда функция выпукла вниз.

Нам не нужно точное построение, поэтому достаточно взять 2-3 точки, и примерно построить. Например, (0;1), (1, -1+√2)≈(1,0.4).